はじめに
統計学では、期待値と並んで重要な分散。言葉の意味からは「散らばり具合」を表すことは分かりますが、散らばり具合とは何なのかということは意外と分かりにくいです。
この記事では、具体例を用いて分散の意味を説明してみます。
図で理解する分散
例えば、2つの機械(機械Aと機械B)を導入して、製品テストを行い、どちらの機械を導入するかを決めることを考えてみましょう。
何回か製品テストを行ったところ、性能の平均値は2つの機械で同じであったとします。
つまり、図で表すと以下のようになったということです。
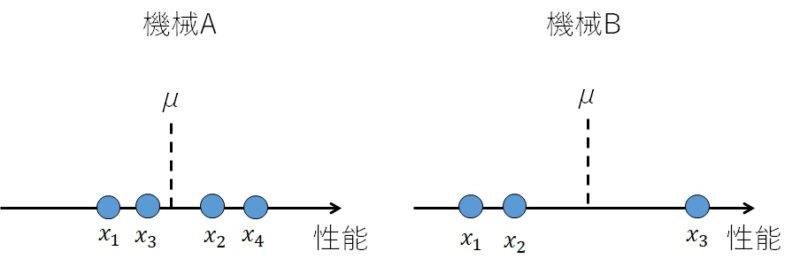
上の図で、\(x_1~x_4\)は製品テストを行って得られたデータで、\(\mu\)はデータの平均とします。
どちらも平均は同じですから、平均だけでは機械AとBのどちらを導入すべきか決められません。
しかし、図から明らかなように、機械Aの方がデータが平均値の近くに集まっており、データに信頼性がありそうだと言うことができます。
この直感的な判断を数字に置き換えたものが分散です。
では、データが平均値の近くに集まっているのを、どのように数字にするのか?
それには、各データと平均値との距離を比べれば良さそうです。
$$V_1=\sum_i |x_i-\mu|$$
数式で表すとこのようになります。つまり、\(V_1\)の値が小さいほどデータは平均の近くに分布し、\(V_1\)の値が大きいほどデータが平均から離れることを意味します。
しかし、絶対値の計算は面倒です。毎回毎回プラスかマイナスかということを確認するのは大変です。
そこで、絶対値ではなく2乗を使用してみましょう。
$$V_2=\sum_i (x_i-\mu)^2$$
こうすると、括弧の中がプラスであろうがマイナスであろうが、2乗すれば必ずプラスになります。
実は、まだ1つ問題が残っています。それは、データの数が大きくなればなるほど、\(V_2\)の値が大きくなることです。
機械AとBの例では、確かに機械Aのデータの方が平均の近くに集まっていますが、データの数が4なので、\(V_2\)の値が機械Bよりも大きくなってしまうかもしれません。
この問題を解決するために、分散はデータの数で割った値が使用されます。
$$\sigma^2=\frac{1}{n} \sum_i (x_i-\mu)^2$$
nがデータの数(機械Aなら4つ、機械Bなら3つ)です。
この式が分散の定義となっています。
分散と標準偏差
続いて、分散と標準偏差について説明します。
例えば先ほどの例で、ある製品の質量[g]を量ったとします。
このとき、分散の定義式
$$\sigma^2=\frac{1}{n} \sum_i (x_i-\mu)^2$$
において、括弧の中が2乗になっているので、製品の質量の単位が\(g^2\)になってしまいます。
グラムの2乗というものに意味はないので、単位を揃えるために標準偏差というものが使われます。
標準偏差は、分散の平方根になっています。
$$\sigma=\sqrt{\frac{1}{n} \sum_i (x_i-\mu)^2}$$
このように定義することで、単位をグラムにすることができます。
おわりに
以上が分散の意味となります。今ではExcel等を使えば分散を計算することは簡単ですが、分散の計算方法を知っていないと、間違った関数を使ってしまったり、計算された値の意味が分からなかったりします。
この機会に是非分散の意味を知っておきましょう!


