推定や検定など様々な場面でお世話になる不偏分散。
本記事では、次の 2 通りの手段を使って、不偏分散を求める方法を解説します。
- エクセル
- 電卓
結論を述べると、エクセルがある場合は一発で計算できてしまいます。
データの数が多い場合は特にエクセルの威力を発揮します。
一方でエクセルなどの表計算ソフトを持っていない方でも、電卓を使って効率よく計算する方法があります。
不偏分散の求め方の公式を知っていれば、電卓をたたく回数を減らして楽に計算することができます。
それでは、エクセルと電卓それぞれの計算方法を見ていきましょう!
エクセルを使った不偏分散の求め方
次のような 10 個のデータの不偏分散を求めてみましょう。
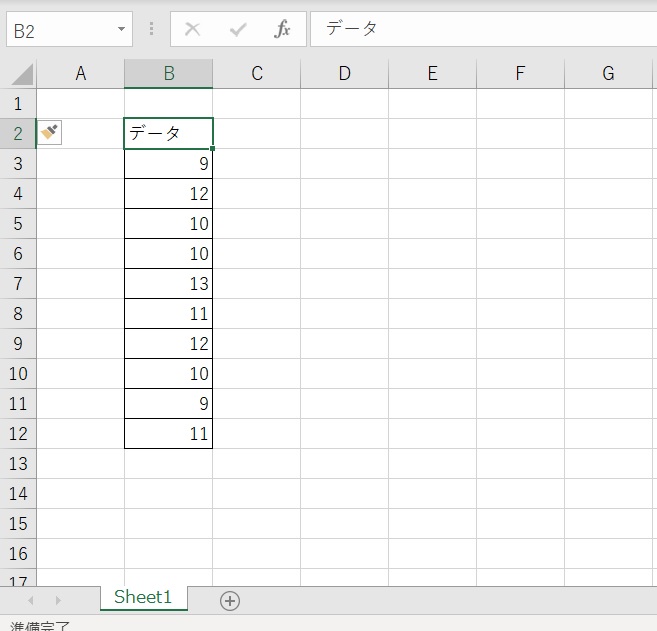
画像のような 10 個のデータがあり、10 個のデータに対して不偏分散を求めます。
エクセルでは不偏分散を求める関数が用意されており、「VAR.S」という関数です。
次のように入力してみましょう。
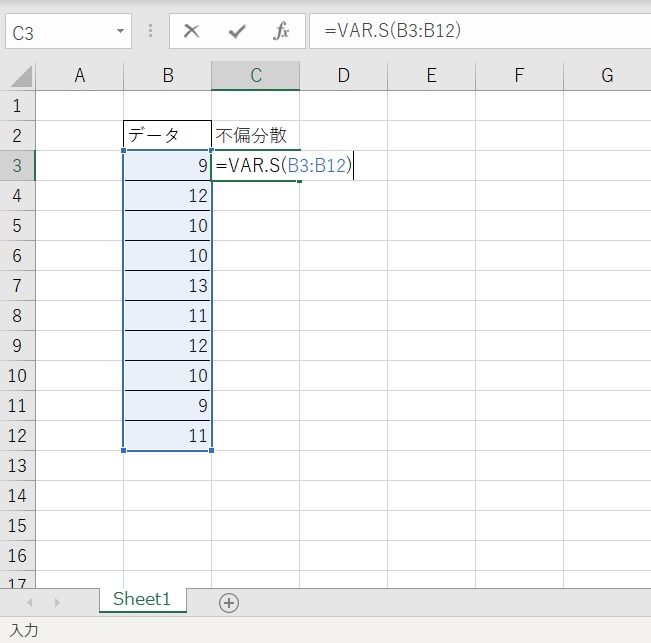
「Enter」キーを押すと、不偏分散の値 1.788… が得られます。
エクセルで計算する最大の利点は、関数ひとつで一瞬で計算できることです。
特にデータの数が多いときに便利です。
電卓を使った不偏分散の求め方
エクセルが使えない環境にある場合、電卓で計算する方法を知っていると効率的です。
電卓を使う場合、不偏分散を下記のように変形した式を用いると、早く計算することができます。
\begin{align}
s^2&=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\\
&=\frac{1}{n-1}\left\{\sum_{i=1}^n x_i^2-\frac{(\sum_{i=1}^n x_i)^2}{n}\right\}
\end{align}
この式を使う場合、次のように計算していきます。
まず、下の画像のように、個々のデータを2乗した値を書きます。
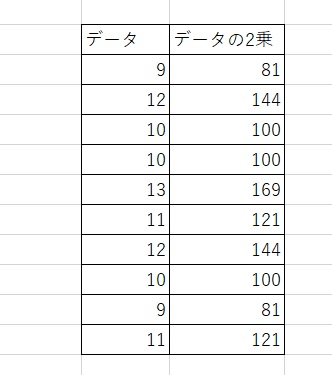
次に、下の画像のように、各列のすべての数字を合計した値を計算してメモします。

データの個数は 10 ですので、上の画像の「合計」の欄と、\(n=10\)を公式に入れて計算できます。
\begin{align}
s^2&=\frac{1}{n-1}\left\{\sum_{i=1}^n x_i^2-\frac{(\sum_{i=1}^n x_i)^2}{n}\right\}\\
&=\frac{1}{9}\left(1161-\frac{107^2}{10}\right)\\
&=1.788\cdots
\end{align}
個々のデータの 2 乗を計算するのが少々手間ですが、電卓を使うとどこでも計算できるのが便利です。
また、不偏分散の式が、実際のデータに対してどのように使われるのかを、感覚的に理解しやすいのも利点です。
不偏分散の結果の解釈
エクセルや電卓を使えば不偏分散を求めることはできますが、不偏分散がどのような意味を持っているのかを理解することは、もっと重要です。
不偏分散を計算するときに起こる間違いとしては、n-1 で割るべきところを誤って n で割ってしまうことです。
不偏分散を計算するときには、n ではなく n-1 で割る理由を理解しておくと良いです。
近年は計算機の発達スピードが速く、大規模なデータでも瞬時に計算することが可能となってきています。
そのため、単に計算できるだけでなく、計算結果をどのように解釈するのかが重要になってきています。
まとめ
本記事では、不偏分散の求め方を、エクセルの場合と電卓の場合それぞれで解説しました。
それぞれの方法にメリットデメリットがあり、以下のようにまとめられます。
| エクセル | 電卓 | |
|---|---|---|
| メリット | ・関数ひとつで計算できる ・データが数が多くなっても労力は変化せず | ・エクセルがなくても計算できる ・不偏分散の式の意味を理解しやすい |
| デメリット | ・エクセルがないと計算できない ・バージョンによっては関数が使えない | ・計算の手間がかかる ・膨大なデータには向いていない |
この記事を見ながら、実際に計算してみましょう!


