データの平均値を推定したり検定したりするときには、正規分布を用いた方法と、t分布を用いた方法があります。
問題の状況によって、正規分布を使うか、t分布を使うか、が決まりますので、本記事で解説します。
t分布と正規分布を使い分ける基準
t分布と正規分布を使い分ける基準は、母分散がわかっているかどうかで判断します。
母分散がわかっているときは正規分布を使用し、母分散がわかっていないときはt分布を使用します。
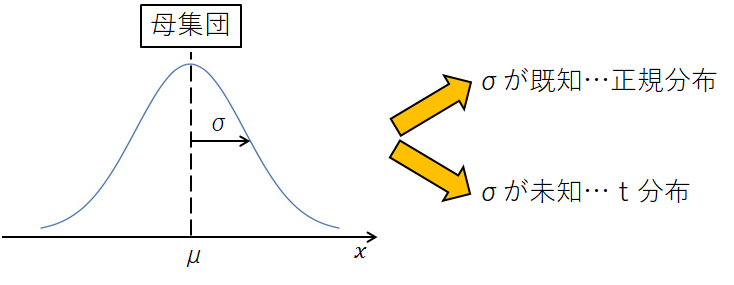
次節以降で、その理由と具体的な例を解説します。
t分布と正規分布を使い分ける理由
さきほどは、母分散が既知か未知かで使い分けることを説明しました。
実は、母分散が既知の場合でもt分布を使用することができます。
つまり、以下の表のように、t分布は母分散の既知・未知にかかわらず使うことができるのです。
| 母分散 | 正規分布を使った推定・検定 | t分布を使った推定・検定 |
|---|---|---|
| 既知 | 〇 | 〇 |
| 未知 | × | 〇 |
では、なぜ母分散が既知のときには正規分布を使うかというと、正規分布を使った方が推定・検定の精度がよいからです。
正規分布はt分布よりも尖った形状をしているので、同じ区間の幅が小さくなります。(下図)
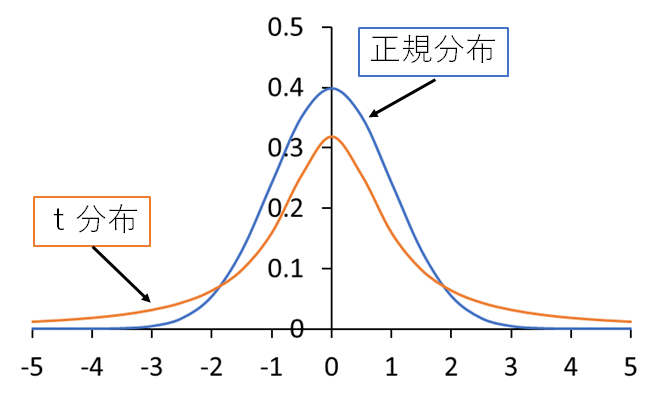
よって、母分散が既知のときには、推測の精度を上げるために正規分布を使う方がよいです。
母分散が既知のときの比較の例
母分散が既知のとき、正規分布を使った場合と、t分布を使った場合とで、推定結果にどのような違いがあるのかを例題で確認してみましょう。
正規分布にしたがう母集団から、データを 6個とった。
21, 20, 23, 20, 20, 19
長年の経験から、母分散は 1.9 であることがわかっている。
母平均の 95% 信頼区間を求めよ。
母分散がわかっていますので、正規分布を用いても、t分布を用いても解くことができます。
比較のために、両方で計算してみましょう。
正規分布の場合
6 個のデータの平均値は 20.5 ですので、母平均の 95% 信頼区間は、
$$20.5-1.96\times \frac{\sqrt{\sigma}}{\sqrt{6}}\leq \mu \leq 20.5+1.96\times \frac{\sqrt{\sigma}}{\sqrt{6}}$$
母分散が 1.9 なので、\(\sigma=\sqrt{1.9}\) を代入して計算すると、
$$19.4\leq \mu \leq 21.6$$
となります。
詳しい計算方法に関しては、母分散が既知のときの区間推定のやり方を参照してください。
t分布の場合
6 個のデータの平均値は 20.5、不偏分散は 1.9 なので、95%信頼区間は、
$$20.5-2.57\times \frac{\sqrt{s}}{\sqrt{6}}\leq \mu \leq 20.5+2.57\times \frac{\sqrt{s}}{\sqrt{6}}$$
不偏分散の値 \(s=\sqrt{1.9}\) を代入して
$$19.1\leq \mu \leq 21.9$$
詳しくは、母分散が未知のときの区間推定のやり方をご覧ください。
結果を見比べてみましょう。
母平均の 95%信頼区間は、
- 正規分布
\([19.4, 21.6]\) - t分布
\([19.1, 21.9]\)
正規分布の方が信頼区間の幅が小さく、推定には都合のよいことが分かります。
このように、母分散がわかっているときは正規分布を使うようにしましょう。
まとめ
本記事では、母平均の推定・検定で、t分布と正規分布を使い分ける基準を解説しました。
結論としては、
- 母分散がわかっている(母分散既知)
正規分布を使う - 母分散がわかっていない(母分散未知)
t分布を使う
です。
母分散の情報が重要ですので、理解を深めたい方は以下の記事も参考にしてください。



