t分布表の使い方や、使いどころが分からずに悩んでいませんか?
本記事では、t分布表とは?というところから始めて、
t分布表をスラスラと読めるようにするために、見方を徹底解説します。
t分布表とは?
t分布表をグラフと図でイメージ
ことばで説明するよりも、図でイメージする方がわかりやすいので、
t分布表を見てみましょう。
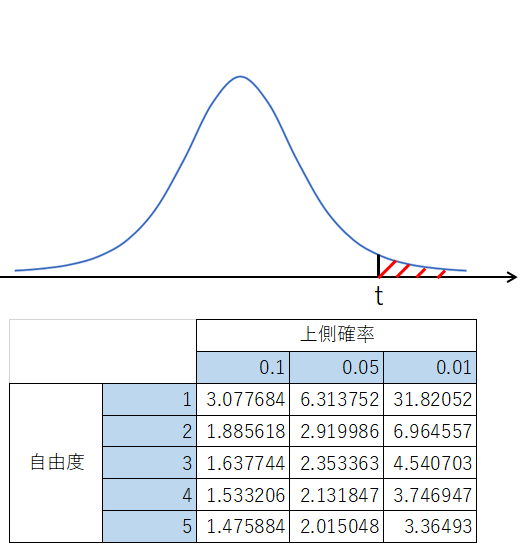
t分布表には、グラフと表がセットでえがかれています。
グラフだけ、あるいは、表だけだと、何も読み取ることができません。
必ず、両方を見る必要があります。
t分布表を読み解くには、t分布表に何が書かれているか
知らなければなりません。
書かれていることが分からないのに、読み解けるわけはありませんからね…
t分布表に書かれていること
t分布表には3つの情報が書かれています。
- 確率
- 自由度
- t値
それぞれ、t分布表の中には、以下の部分に書かれています。
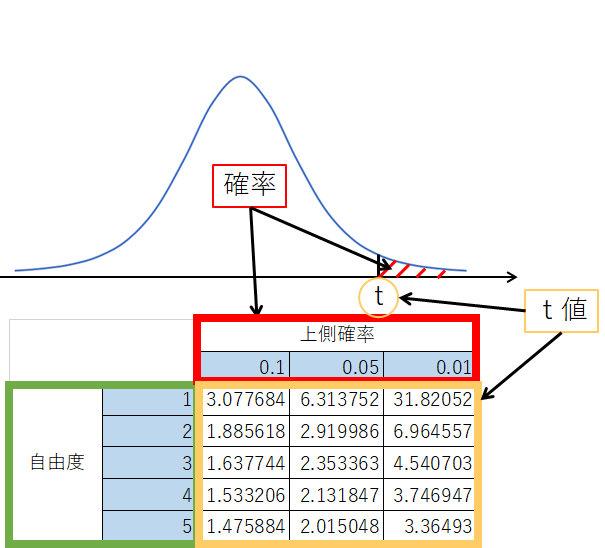
確率、自由度、t値の書かれている場所は、
- 確率…グラフの中の斜線と、表の横の見出し
- 自由度…表の縦の見出し
- t値…グラフの横軸と、表の中の計算結果
確率とt値は、グラフの中と、表の中に書かれており、グラフと数値が対応しています。

自由度は表の中だけ?
グラフの中にはないの?
と思われるかもしれません。
じつは、自由度はグラフの形状を決めています。
しかし、t分布表を読み取るときには、グラフの形状を考える
必要はないので、「表の中に書いてある」とだけ覚えておいて問題ありません。
t分布が使われる場面
t分布表が読めるようになっても、どこで使えるかわからなければ意味がありません。
そのため、t分布がよく使われる場面をご紹介します。
t分布がおもに使われるのは、次の2つです。
- 母分散がわからないときの区間推定
- 母分散がわからないときの仮説検定
母分散とは、「考えている集団全体のばらつきの程度」です。
「区間推定」や「仮説検定」がどういうものであるかは、後ほど具体例を使って解説します。
t分布表が使える場面は、たくさんのデータを取ってきて、データの平均値がどのくらいになりそうか、を推測するときです。
平均値を求めたいということは多いため、t分布表は活躍の場所が多いです。
t分布表の見方の基本
いよいよ、t分布表の見方を学んでいきましょう。
…その前に、t分布表には「上側確率」と「両側確率」の2種類があります。
それぞれで使い方が少し異なるため、違いをおさえてから、
t分布表の使い方をチェックしましょう。
t分布表の種類
さきほどお示ししたように、t分布表には「上側確率」と「両側確率」の2つが存在します。
なぜ2種類あるのかと言うと、作成者の好みが分かれるからです。
「上側確率」と「両側確率」のどちらを用いても計算できますが、
教科書やサイトによってバラバラですので、「上側確率」か「両側確率」かは確かめておきましょう。
さて、「上側確率」と「両側確率」の違いをご説明します。
上側確率とは、グラフの右側の確率を表にしたものです。
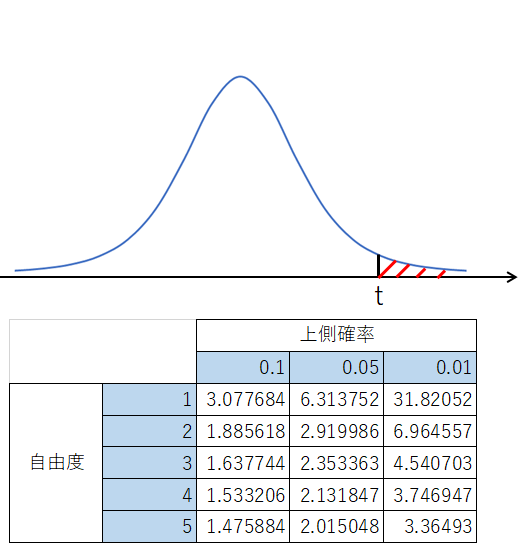
上側確率がのっている表では、グラフの右側1%、5%、10%の値が書いてあります。
対して、両側確率は、グラフの右側と左側の確率を足した値が表に書いてあります。
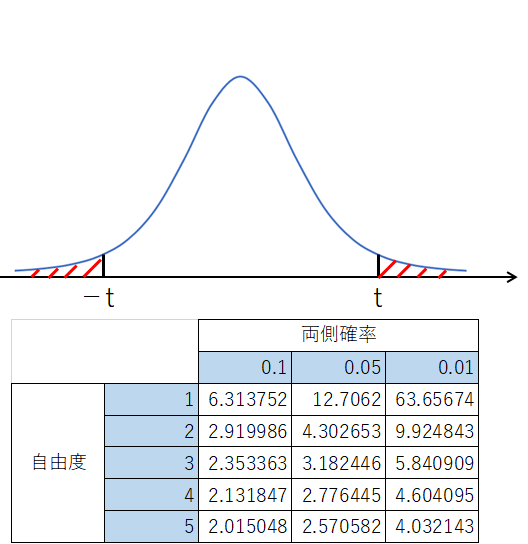
表の中の1%、5%、10%という数値は、グラフ両側の斜線部分を足した値です。
2つを使い分けると混乱するので、本記事の以降では、すべて「上側確率」のt分布表を使って解説します。
t分布表の読み取り方
「上側確率」のt分布表を使って、t分布表の見方を理解していきましょう。
t分布表の見方は非常にシンプルです。
問題を解くときに、確率と自由度がわかりますので、確率と自由度が交差する値を読みます。
たとえば、自由度3、上側確率 0.05 のとき、図を見ると、交差した値が読み取れます。
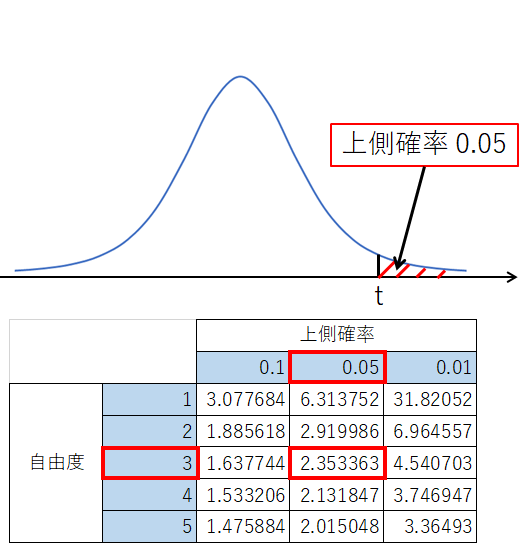
交差している値を読むと、2.35 となっています。
2.35 という値は、グラフの中のtの値のことです。(下図)
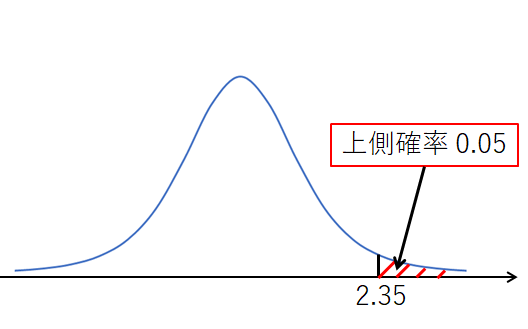
t分布表を読み取る手順はたったこれだけです。
つまり、「上側確率が 0.05 となる横軸の値は 2.35」と求めるのが、t分布表の使い方になります。
といっても、具体例がないとイメージしにくいです。
そのため、t分布がよく使われる「区間推定」と「仮説検定」の例題を用意しました。
例題を見て、使い方を覚えていきましょう。
t分布表の使用例【区間推定】
10 個の製品の重さをはかったところ、平均値 23g、不偏分散が 3gであった。
製品の母平均(真の平均)を \(\mu\) とすると、
$$T=\frac{23-\mu}{\sqrt{3/10}}$$
は自由度 9 のt分布にしたがう。
T の90%信頼区間を求めよ。
例題のような区間推定の問題は、t分布表を使う練習に最適です。
長々と問題文が書かれていますが、重要な部分は1つだけです。
(中略)
…自由度 9 のt分布にしたがう。
T の90%信頼区間を求めよ。
残りの部分は、問題の状況を理解してもらうために作りました。
自由度9のt分布ですので、下図の交差する点を読みます。
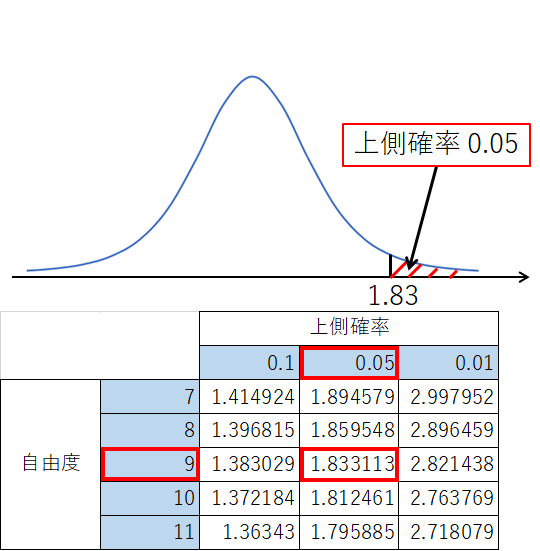
なぜ 0.05 の列を読むかというと、上側確率 0.05 のとき、グラフの左側も同様に 0.05 となるので、あわせて 10% になるからです。
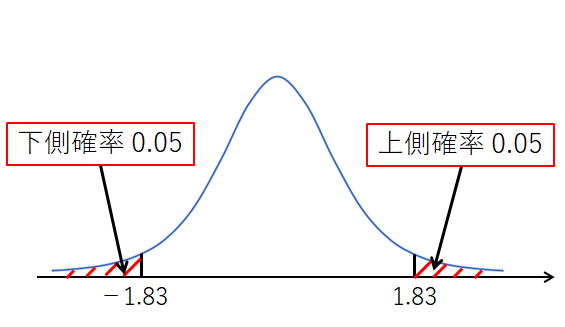
よって、T の 90% 信頼区間は、
$$-1.83\leq T\leq 1.83$$
となります。
t分布表の使用例【仮説検定】
10 個の製品の重さをはかったところ、平均値 23g、不偏分散が 3gであった。
製品の母平均(真の平均)を \(\mu\) として、母平均が 20g より大きいか知りたい。
$$T=\frac{23-20}{\sqrt{3/10}}$$
とおくと、T は自由度 9 のt分布にしたがう。
有意水準 1%として、T の棄却域を求めよ。
仮説検定の問題では、「母平均が 20g より大きいか」ということを計算で求めることができます。
有意水準 1% ですので、t分布表で自由度 9 と、上側確率 0.01 が交差するところを読み取ります。
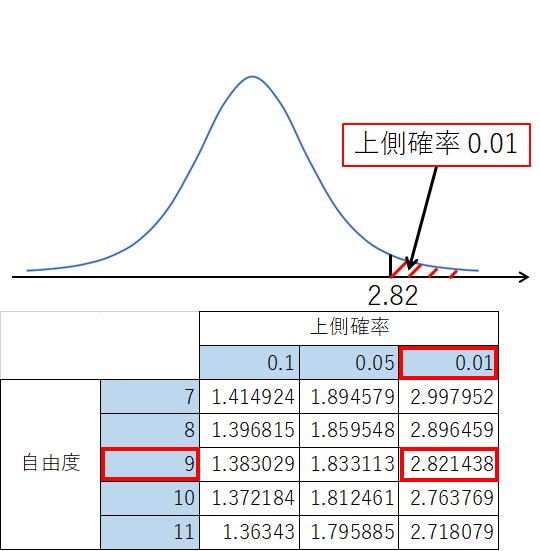
交差する値は 2.82 ですので、有意水準 1% の棄却域は、
$$T\geq 2.82$$
ということがわかります。
T が 2.82 よりも大きければ、「母平均が 20g である」という可能性は低いので、「母平均が 20g 以上である」と導くことができます。
まとめ
本記事では、t分布表の使い方を解説しました。
t分布表には、
- 確率
- 自由度
- t値
の3つの情報が書かれています。
t分布表でできることは、確率と自由度を使ってt値を求めることです。
t分布表があれば、たくさんのデータの平均値を予測することができます。
「手元にt分布表がなくて、いちいち探すのが大変」
という方は、エクセルを使ってt分布表を作っておくと良いです。
t分布のグラフの描き方と、t分布表の作り方は下記記事で紹介していますので、ぜひ参考にしてください。



