前提:仮説検定の考え方
有意水準と検出力は、仮説検定という分野で出てきます。
まずは、仮説検定の基本を知るために例題を見てみましょう。
あなたは新しい薬を開発しました。
今まで販売されていた薬とくらべて、新薬に効果があるかどうかを試したいです。
このとき、統計では、「帰無仮説」「対立仮説」という2つの仮説をたてます。
- 帰無仮説:新薬は今までの薬と効果量が同じである(つまり、効果がない)
- 対立仮説:新薬は今までの薬とくらべて、効果量が高い(つまり、効果がある)
薬の効果は人によって違うので、被験者をたくさん集めて効果量をはかります。
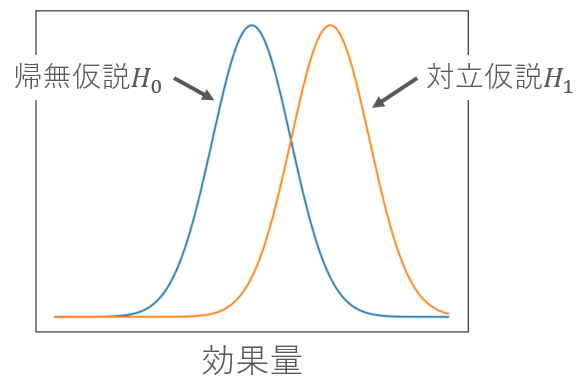
実際にデータを集めると、上図のようになります。
帰無仮説は今までの薬を与えられたグループ、対立仮説は新薬を与えられたグループです。
図を見ると、新薬は効果がありそうに見えますが、本当にそうでしょうか。
人によって効果が違うので、たまたま差があるように見えただけかもしれません。
この場合、新薬は本当に効果があるのかどうかをはかるのが仮説検定です。
図でわかる有意水準と検出力
前節では帰無仮説と対立仮説を紹介しました。もう一度書くと、
- 帰無仮説:新薬は今までの薬と効果量が同じである(つまり、効果がない)
- 対立仮説:新薬は今までの薬とくらべて、効果量が高い(つまり、効果がある)
この2つの仮説があるとき、判断のしかたによって、次の表のように4つの場合があります。
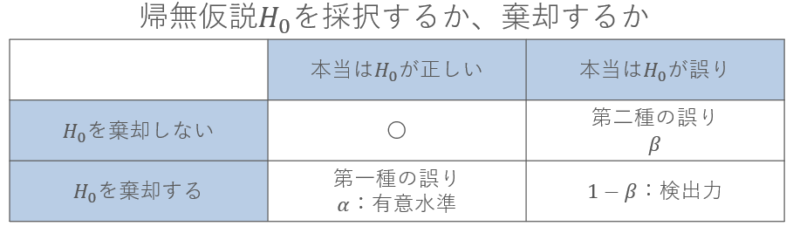
つまり、真実は新薬の効果がないにもかかわらず、新薬は効果があると判断してしまうことを「第一種の誤り」といいます。
反対に、本当は新薬は効果があるのに、効果があるとは言えないと判断してしまうことを「第二種の誤り」といいます。
そして、第一種の誤りをおかす確率の基準値を有意水準、第二種の誤りをおかさない確率のことを検出力とよびます。
グラフにすると次のようになります。
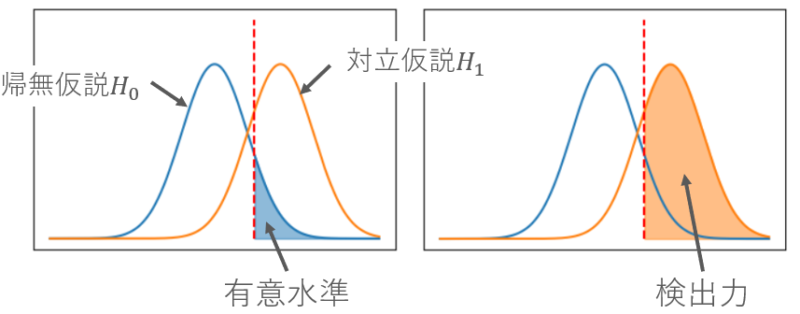
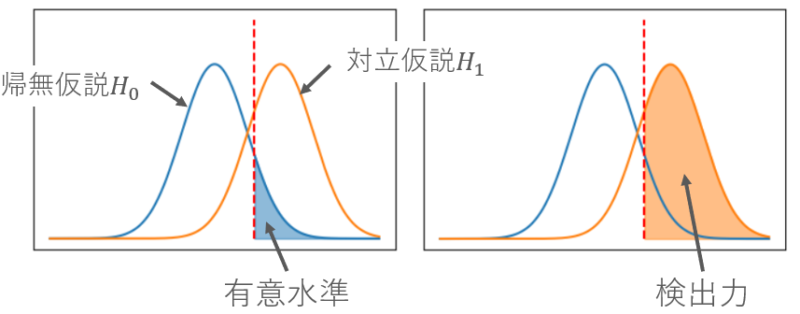
上図を解説します。
2つの山は帰無仮説と対立仮説の分布をあらわしていて、縦の破線は閾値をあらわしています。
縦線よりも左の値は、帰無仮説を棄却せず、縦線よりも右の値は、帰無仮説を棄却します。
そして、有意水準とは帰無仮説が正しいのに、帰無仮説を棄却してしまう確率のことなので、図で示した部分の面積になります。
検出力は帰無仮説がまちがっているときに、正しくまちがっていると判断する確率なので、図の右側で示した面積になります。
よい分析をするために基準をどう設定すればいいのか
有意水準と検出力は、理解がむずかしいので、図で覚えてしまいましょう。
さて、有意水準と検出力をどのように設定すればいいのかを説明します。
まず最初に、有意水準をさきに決めてしまいます。ビジネス要件にもよりますが、一般的には、有意水準は5%とします。
すると、上図の縦線の位置が決まるので、検出力は自動的に決まってしまいます。
検出力は80%か90%以上あれば、信頼できる仮説検定といわれることが多いです。
しかし、検出力は自動的に決まってしまうのに、どうやって80%、90%以上にするのか、と思ったかもしれません。
検出力を上げるひとつ目の方法は、効果量を大きくすることです。
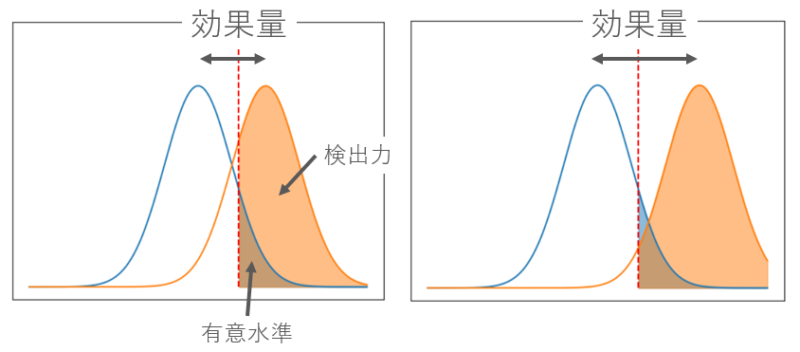
右の図は左とくらべて効果量が大きくなっています。
左右の図はどちらも同じ有意水準ですが、明らかに右のほうが検出力の面積が大きくなっています。
このように効果量を大きくすることで、検出力が上がって信頼できる結果となります。
しかし、実際に効果量を大きくするには、今までの薬とくらべて良い薬を開発することと同じなので、簡単にできることではありません。
そこで、検出力を上げるもうひとつの方法を紹介します。
それは、サンプルサイズを大きくすることです。つまり、取得するデータの数を大きくします。
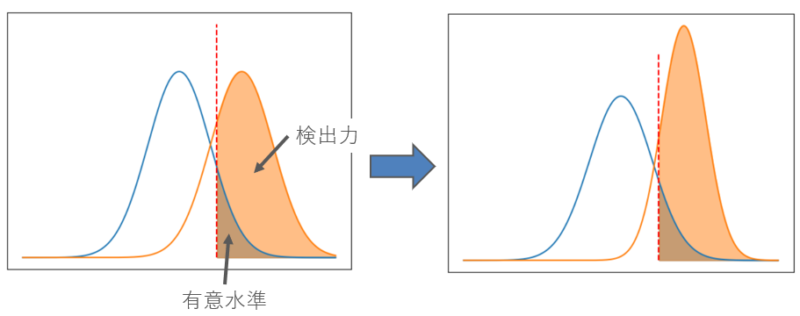
サンプルサイズを大きくすると、データが中心のまわりに集まります。これを大数の法則といいます。
図を見てわかるように、分布の山が細くなることで、検出力の面積が大きくなっています。
以上、検出力を上げる方法を2つみてきました。
効果量の大きい新薬で試験できるなら、データの数が小さくても信頼できる結果が得られます。つまり、試験のコストをおさえることができます。
反対に、効果量の変化が小さい新薬では、検出力を上げるために、たくさんのデータをとらなければいけません。
まとめ
本記事では、有意水準と検出力を解説しました。これらは仮説検定で使われます。
- 有意水準:ほんとうは帰無仮説が正しいのに、棄却してしまう確率をあらわしています。
- 検出力:帰無仮説がまちがっているときに、正しく棄却する確率をあらわします。
仮説検定をおこなうときには、最初に有意水準を5%などで決めて、検出力が80%または90%以上あったら信頼できる結果としてあつかいます。
有意水準を決めたら検出力は自動的に決まってしまいますが、検出力を上げるために、効果量の大きい仮説検定をおこなったり、サンプルサイズを大きくすることが効果的です。