統計の理論で使われる「再生性」。
再生性の意味と、使われ方を図で分かりやすく説明します。
図で理解する正規分布の再生性の意味
一言で説明するならば、「正規分布からデータを得たとき、そのデータの和もまた、正規分布に従う」となります。
これはどのような意味を持っているのか、図を見てみましょう。
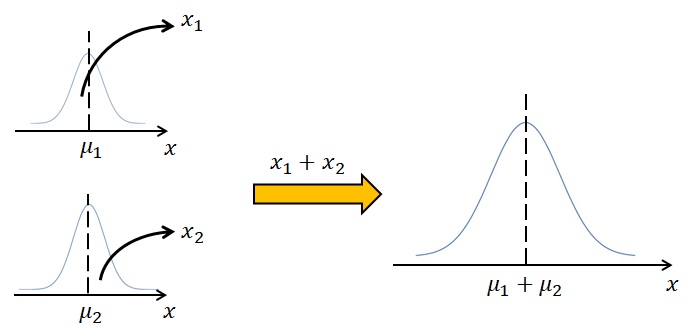
左のグラフのように、平均 \(\mu_1\)、分散 \(\sigma_1^2\) の正規分布 \(N(\mu_1,\sigma_1^2)\) と、別の正規分布 \(N(\mu_2,\sigma_2^2)\) からそれぞれデータ\(x_1\) と \(x_2\)を得たとします。
すると、2 つのデータの和 \(x_1+x_2\) は、平均 \(\mu_1+\mu_2\)、分散 \(\sigma_1^2+\sigma_2^2\) の正規分布 \(N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)\)に従います。
図では 2 つの正規分布を使いましたが、同じ正規分布からデータを 2 個取ってきた場合でも再生性は成り立ちます。
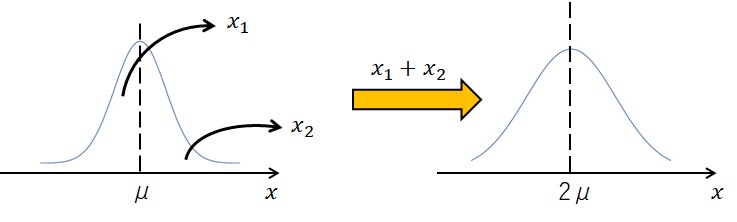
この場合、正規分布 \(N(\mu,\sigma^2)\) から 2 つのデータを取ってきて、その和をとると、\(x_1+x_2\) は \(N(2\mu,2\sigma^2)\) に従います。
重要なことは、正規分布から得た 2 つのデータの和もまた正規分布に従うということで、これを「再生性」と呼びます。
正規分布の和の分布も正規分布に従う、というのが再生性の大きなポイントです。
ちなみに、再生性はすべての分布で成り立つわけではなく、正規分布や二項分布などの一部の分布にのみ成り立ちます。
続いて、正規分布に再生性があると、どのような利点があるかについて説明します。
再生性が成り立つことによる利点
正規分布の再生性が最もよく用いられるのは、統計的推測や検定です。
以下では、再生性が使われる例として、平均値を求める意味について取り上げます。
例えば、長さ、電流、温度など、知りたい真の値(これを母平均と呼びます)を求めるために、測定を複数回行うとします。
このとき、複数回の測定の平均値を採用すると思いますが、「なぜ平均値を使うのか」ということを疑問に思ったことはないでしょうか。
測定の平均値を使って真の値を推定するときに用いられるのが、再生性の考え方です。
3 回の測定を行ったとき、それぞれの測定値は正規分布 \(N(\mu,\sigma^2)\) に従っていると考えられ、再生性の考え方より、3 回の測定の平均値は正規分布 \(N(\mu,\sigma^2/3)\) に従います。
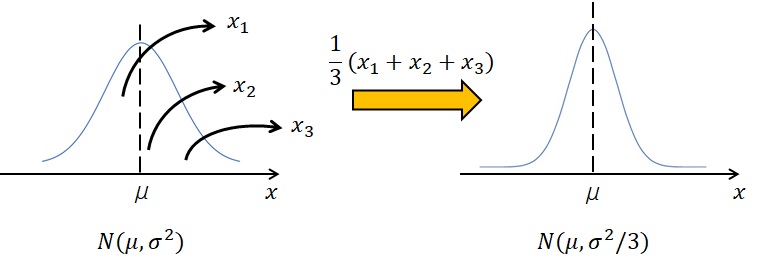
上図において、本当に求めたいのは左側の分布の真の平均値 \(\mu\) です。
図の右側ように、3 回の測定の平均値も正規分布になって、さらに分散が小さくなるので、真の平均値 \(\mu\) に近づきます。
つまり、繰り返し測定を行って測定の平均値を計算すると、真の平均値 \(\mu\) に近づきます。
その根拠を与えているのが、再生性の考え方です。
まとめ
本記事では、正規分布の再生性について解説しました。
再生性とは、「正規分布からデータを取ってきて、それらの和を取るとまた正規分布になる」ということです。
再生性は統計的推測や検定の理論を支える大切な性質です。
ここで考え方を理解していただければ幸いです。
以上、正規分布の再生性の意味とそのメリットについてでした。


