「母分散の既知や未知ってそもそも何?」
「信頼区間を計算するときには何が違うの?」
「計算結果はどう変わるの?」
本記事では、上記のような疑問に答えます。
母分散の既知・未知とは何か
母分散とは、集団全体のばらつきの程度を表す数値で、集団全体が平均に近いかどうかを見ることができます。
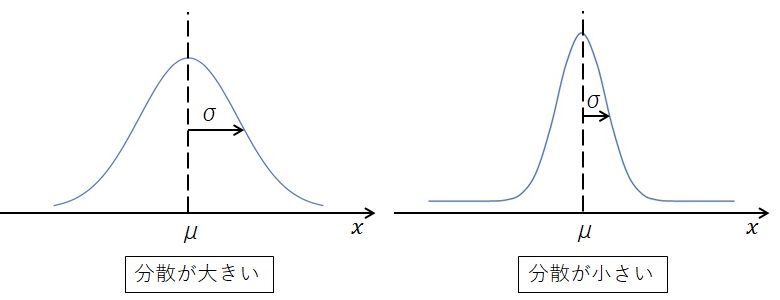
では母分散の既知・未知とは何を示しているのでしょうか?
既知とは「すでに知っている」、未知とは「まだ知らない」という意味で、母分散があらかじめ分かっているかを表します。

母分散をすでに知っている、という状況は存在するの?
と思われるかもしれませんが、お察しの通り、母分散があらかじめ分かっている状況というのは稀です。
具体的には、長年のデータの蓄積により、集団全体のデータの散らばり具合が分かっているとき等の特殊な状況だけです。

そうしたら母分散既知の計算方法を学習する意味は?
確かに母分散既知の場合は少ないですが、母分散「既知」の計算方法を理解していないと、母分散「未知」の計算方法を理解するのは困難です。
そのため、統計学の教科書には、母分散既知の場合と未知の場合の両方の計算手順が載っていることが多いです。
信頼区間の計算方法の比較
集団全体が正規分布に従っている場合について説明します。
信頼区間を求めるときには、母分散が分かっているかどうかで、計算方法が異なります。
n 個のデータの平均値を \(\bar{X}\)、母分散を \(\sigma^2\)、不偏分散(データから計算できます)を \(s^2\)とすると、母平均 \(\mu\) の信頼区間は以下のように求められます。
$$既知:\bar{X}-Z \frac{\sigma}{\sqrt{n}}\leq \mu \leq \bar{X}+Z \frac{\sigma}{\sqrt{n}}$$
$$未知:\bar{X}-t \frac{s}{\sqrt{n}}\leq \mu \leq \bar{X}+t \frac{s}{\sqrt{n}}$$
Z とtは「信頼係数」と呼ばれる値で、どのくらい精度の高い信頼区間を求めたいかによって変化します。
式のポイントは形が同じということです。既知でも未知でも同じような式を使うことができ、代入する値を変えるだけで計算できます。
それぞれの具体的な計算方法は下記の記事をご覧ください。
既知と未知とで信頼区間が異なる理由
一般に、母分散が既知の方が、未知よりも信頼区間が狭くなります。
信頼区間が異なる理由を2通りの方法で説明します。
1つ目の理由は、既知の方が、未知と比べて情報量が多いからです。
つまり、既知の場合には「母分散」という、集団全体のばらつきの程度が分かっているので、そのぶん多くの情報を持っていることになります。
情報量が多いということは、精度よく推定できるはずですので、信頼区間が狭くなります。
2つ目の理由は、信頼区間の計算に使われる分布が異なるからです。
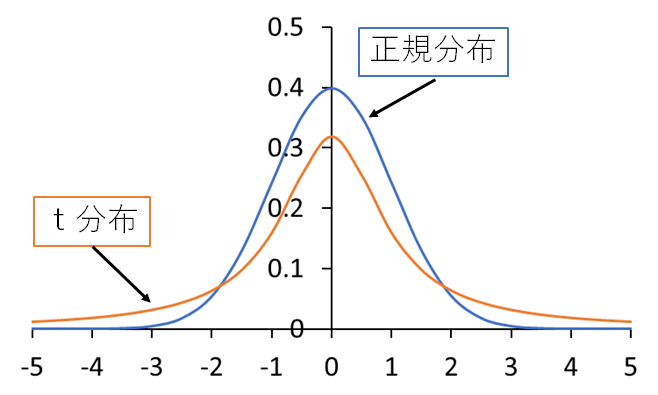
既知の場合は「正規分布」が使われ、未知の場合は「t分布」が使われます。
下図のように正規分布とt分布を重ねると、t分布の方が裾が広いことが分かります。
よって、未知の方が信頼区間の幅が広くなります。
まとめ
本記事では、母分散が既知(わかっている)と、未知(分かっていない)の場合の違いを解説しました。
母分散が分かっているかどうかで、信頼区間の計算方法が異なります。
計算式は同じ形をしていますが、代入する値が異なりますので、信頼区間の幅も違います。
信頼区間を求めるときには、「母分散が分かっているか?」ということに意識を向けると良いです。


