「この製品は 3σ を超えているから不合格」
「この計測結果は 2σ に入っているから問題なし」
このような σ の使い方を聞いたことはありませんか?
専門用語を使っているので難しそうに聞こえますが、中身は非常にシンプルです。
本記事では、σ の意味を説明し、あなたが明日から σ を使った会話についていけるようにします。
正規分布の σ とは
まず、σ は「シグマ」と呼びます。この文字はギリシャ文字であり、σ の大文字は ∑ と書きます。
統計学では一般に、σ は標準偏差を表します。
標準偏差は分布の広がり具合を表し、正規分布では下図のようになります。
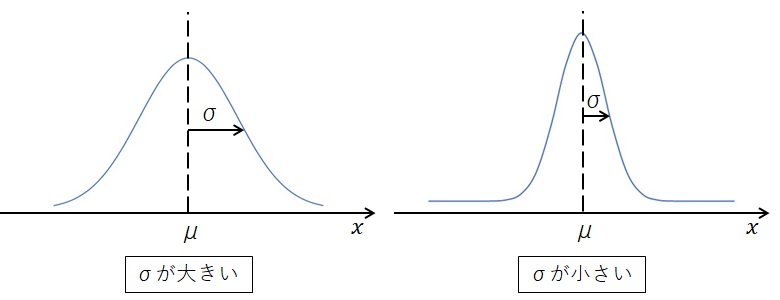
図を見ていただけると分かるように、σ が大きいほど分布の形状は滑らかになります。
例えば、ある製品を大量に作って質量を測ったとします。
すべての製品が全く同じ質量になることはありませんから、横軸に質量を取り、縦軸に個数を取った場合には、上図のようになるでしょう。
このとき、図の右側のように、平均値付近の質量の個数が多ければ、σ が小さくなります。
正規分布の場合には σ の値が分かるだけで分布の広がり具合を特定できることから、重要な指標となります。
σ のイメージをつかめましたでしょうか?
次の節では図を使って1σ、2σ、3σ について説明していきます。
1σ、2σ、3σ の使い方
初めに 1σ について説明します。
1σ とは正確に述べると\(\mu\pm\sigma\)のことです。
図で表すと、下図の斜線の部分のことを指します。
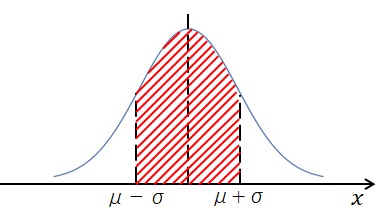
斜線部の面積は全体の約68%となっています。
すなわち、1σ とは
「平均値のまわり約68%が入る区間\(\mu\pm\sigma\)」
のことを指します。
例えば多数の製品の質量が、平均値 30g、標準偏差 2gの正規分布に従っていたとします。
この場合、1つの製品を取り出して質量を測定したとき、30g±2g(つまり28~32g)に含まれる確率は約68%ということです。
取り出した製品の質量が31.5gであったなら、「この製品は 1σ に含まれている」と表現することになります。
続いて 2σ について説明します。
考え方は 1σ の場合と全く同じで、\(\mu\pm2\sigma\)の区間のことを表します。
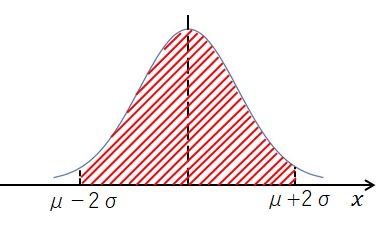
2σ に含まれるのは、上図の斜線部で、その面積は全体の約95%です。
工場などで大量生産する場合には 2σ が規格値として採用されることもあります。
2σ を製品出荷の規格とした場合、100個の製品を作ると約5個が不良品として処分されるということです。
3σ も全く同様で、\(\mu\pm3\sigma\)の区間のことです。
この区間内の面積は全体の約99.7%で、3σ から外れることはめったにありません。
製品の出荷や実験の測定などで 3σ を超える値が検出された場合は異常と判定されることが一般的です。
ここまで1σ、2σ、3σ について説明してきました。
σ は、測定された値が外れ値であるかどうかを調べるために用いられることが多いです。
さすがに 1σ の範囲外(約32%)を外れ値と考える人はいないと思いますが、外れ値とは2σ の範囲外(約5%)であるか、 3σ の範囲外(約0.3%)であるか、ということは意見が分かれると思います。
この問題に対する答えはなく、効果・安全性・コストなどの面を考慮して個別に判断されます。
統計学では 2σ、3σ の範囲が何%かということは計算できますが、閾値として何が妥当であるのかということには答えられません。
また、今まで述べてきた σ に関する内容はすべて正規分布に対して計算されたものですので、データを多く集めたときに明らかに正規分布と見なせない場合には 2σ、3σ を使わない方が良いです。
まとめ
本記事では、正規分布の 1σ、2σ、3σ について、その意味を説明しました。
これらの σ は外れ値の検出に用いられることが多く、それぞれ
\(\mu\pm\sigma\)の区間に入る確率は約68%
\(\mu\pm2\sigma\)の区間に入る確率は約95%
\(\mu\pm3\sigma\)の区間に入る確率は約99.7%
です。
直感で外れ値の判断基準を決めるよりも σ を使って決める方が説得力がありますし、知的な印象を与えられるかもしれません。
これを機に、内容を理解して 1σ、2σ、3σ を使ってみましょう。


