モーメント母関数は統計の理論を理解するためには必要で、期待値や分散の導出、再生性の証明などに使われます。
ほとんどの確率分布に対してモーメント母関数を計算することができますが、正規分布のモーメント母関数を計算するのは容易ではありません。
筆者もモーメント母関数の定義式を使って計算してみたことがありますが、初めて計算したときは、計算途中で何をしているのか分からなくなってしまいました。
そのため本記事では、どのような方針で正規分布のモーメント母関数を計算していくのかを詳しく説明します。
モーメント母関数と正規分布の定義
次の節から具体的に計算していきますが、まずここでは、正規分布とは何か、モーメント母関数とは何かについて見ていきましょう。
正規分布の確率密度関数は以下のように表されます。
$$f(x)=\frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$$
この式の成り立ちに興味がある方は、正規分布の成り立ちに関する記事をご覧ください。
モーメント母関数を計算するときには、\(\mu\)と\(\sigma\)は定数と見なして、\(x\)のみを変数として扱います。
続いて、モーメント母関数は以下のように定義されます。
$$M(t)=E(e^{tX})=\int_{-\infty}^{\infty} f(x)e^{tx} dx$$
この定義式の\(f(x)\)の部分に上記の確率密度関数の式を入れるのですが、一目で難しそうだと分かりますね。
この記事を読んでくださっているあなたが拒否反応を起こさないように、できるだけ丁寧に解説していきますので、ぜひ最後まで目を通してください。
モーメント母関数の計算
前節で正規分布とモーメント母関数を定義しましたので、具体的に計算していきます。
まずは指数関数について成り立つ式
$$e^a\cdot e^b=e^{a+b}$$
を使って、正規分布のexpの部分と、モーメント母関数のexpの部分を一つにまとめます。
\begin{align}
M(t)&=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \exp(tx) dx\\
&=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}+tx\right) dx
\end{align}
続いてexpの中を\(x\)に関して平方完成を行います。
平方完成とは、\((x+〇)^2\)の形に変形することです。中学数学では、2次方程式の解の公式を導くときに使われています。
なぜ平方完成するかということは、後ほど説明します。
\begin{align}
M(t)&=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} \exp\left\{-\frac{1}{2\sigma^2} (x^2-2\mu x-2\sigma^2tx+\mu^2)\right\}dx\\
&=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{1}{2\sigma^2} \left\{x-(\mu+\sigma^2t)\right\}^2+(\mu t+\frac{1}{2} \sigma^2t^2)\right)dx\\
&=\exp(\mu t+\frac{1}{2} \sigma^2t^2)\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{1}{2\sigma^2} \left\{x-(\mu+\sigma^2t)\right\}^2\right)dx
\end{align}
上式の最後の行について、\(x\)が入っていない項については、積分の前に出すことができます。
このように平方完成を行った理由は、\(x\)が入っている項と、入っていない項を分けるためです。
ここで積分の中をよく見ていただきたいのですが、何となく正規分布の確率密度関数に似ていないでしょうか。
実は積分の中は、平均\(\mu+\sigma^2t\)、分散\(\sigma^2\)の正規分布の確率密度関数になっています。
正規分布の定義式と見比べていただくと、平均だけが変わっていることが分かります。
これを図で表すと下図のようになります。
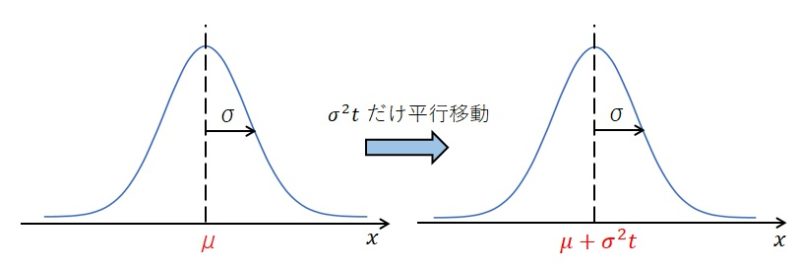
つまり、最後の式の積分は、正規分布を全区間で積分していることになります。
正規分布は確率分布ですので、全区間で積分すると 1 になります。
よって、モーメント母関数は以下のように表されます。
$$M(t)=\exp(\mu t+\frac{1}{2} \sigma^2t^2)$$
長々と計算してきましたが、計算手順は以下のようになっています。
- 指数関数を1つにまとめる
- 平方完成する
- 正規分布を全区間で積分すると 1 になる性質を使う
特に平方完成するときに計算ミスを起こしやすいです。
ちなみに、標準正規分布N(0,1)のモーメント母関数は、\(\mu=0\)、\(\sigma^2=1\)を代入して、
$$M(t)=\exp\left(\frac{1}{2}t^2\right)$$
となります。
標準正規分布のモーメント母関数は、中心極限定理の証明など、時々使われますので、理論をしっかりと学んでおきたいという方は知っておいても良いと思います。
まとめ
本記事では正規分布のモーメント母関数の計算手順を、途中式を多く使いながら説明しました。
モーメント母関数は
$$M(t)=\exp\left(\mu t+\frac{1}{2} \sigma^2t^2\right)$$
と計算され、この式自体は調べるとすぐに出てくると思います。
しかし、理論を理解する上では導出できた方が良いので、自分で計算してうまくいかなかった、という方に少しでも参考になれば幸いです。
以上、正規分布のモーメント母関数の計算についてでした。


