「正規分布表を見るとたくさんの数字が並んでいるけど、見方が分からず計算できない…」
こんな悩みを抱えていませんか?
本記事では、初めて正規分布表を見る人を念頭に置いて、使い方を分かりやすく解説します。
正規分布表とは
そもそも正規分布表とは何でしょうか?
正規分布表とは、「期待値 0、分散 1 の正規分布の面積を計算した図表」のことです。
統計学の教科書の巻末に記載されていることが多く、「正規分布表」で検索すると見ることができます。
ちなみに図表の上に「標準正規分布表」と書かれていることも多いです。
標準正規分布とは期待値 0、分散 1 の正規分布のことであり、「正規分布表」は「標準正規分布表」を省略した言葉です。
正規分布表には以下のようなグラフと数表が書かれています。
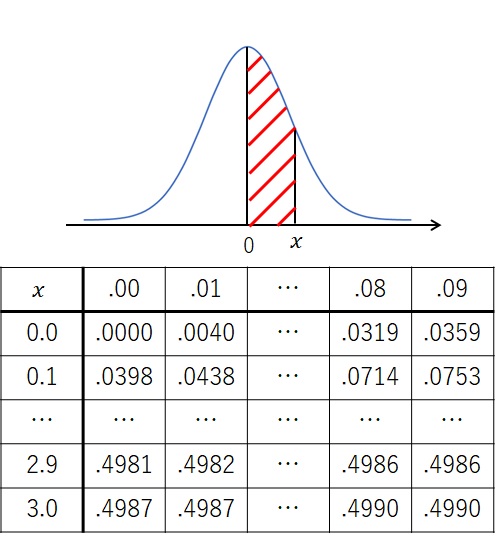
表の一部を抜粋
図の斜線部の面積が確率を表します。
グラフの下の数表には斜線部の面積を計算した結果が書かれています。
表に計算結果が書かれていますので、自分で面積(=確率)を計算する必要はありません。
次節では、正規分布表を使う手順をひとつずつ解説します。
正規分布表の見方の具体的な手順
\(x\) は期待値 0、分散 1 の標準正規分布に従っている。
\(0<x<1.24\)となる確率を求めよ。
最も基礎的な問題になりますので、丁寧に解説していきます。
この例題は以下の手順で解くことができます。
正規分布表のグラフを見て、どこの面積が計算されているかを確認する
意外と見過ごされがちですが、非常に重要なポイントです。
正規分布表にはグラフが描かれており、下図のようなパターンがあります。
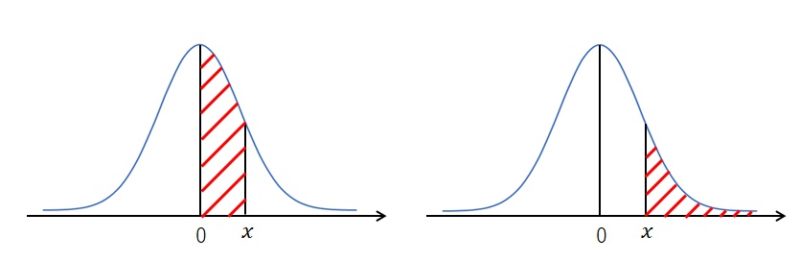
まずはグラフを見て、どの部分に色が塗られているのかを確認しなければなりません。
基本は左のグラフの場合と、右のグラフの場合の 2 種類です。
教科書やウェブサイトによって違うので、表を見る前にグラフを見ることが必須です。
当然ですが、左のグラフと右のグラフの面積は異なるからです。
このページでは、左のグラフをもとに解説します。
問題文が指し示す面積をイメージする
「手順1」では、教科書やウェブサイトにすでに描かれているグラフを確認しました。
「手順2」では、問題文を見て、自分でどの部分の面積を計算する必要があるかを確認しなければなりません。
この例題では、「\(0<x<1.24\)となる確率」を求めるので、下図の面積を求めればよいことが分かります。
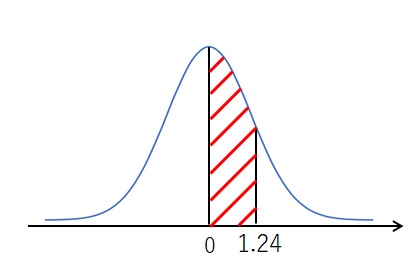
もう一度、正規分布表と、例題で示されている「\(0<x<1.24\)となる確率」を並べて見てみましょう。
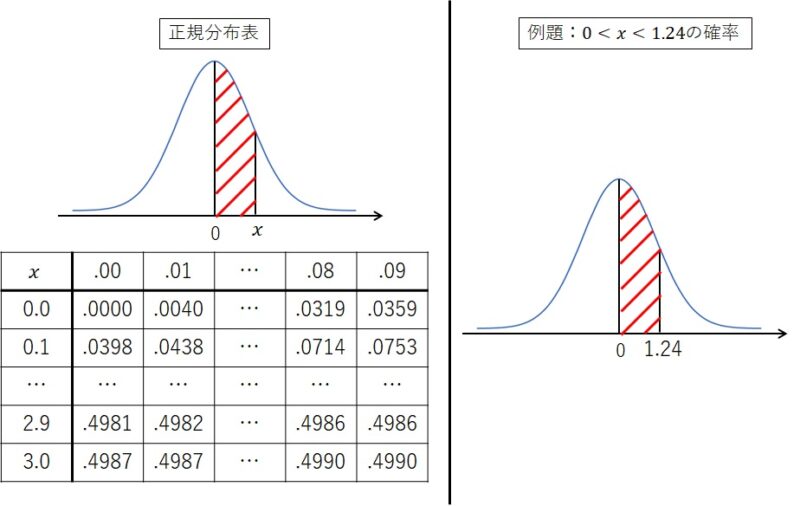
左側が正規分布表で、教科書やウェブサイトに載っています。
右側が例題をもとに、求める確率を図示したものです。
左右のグラフを見比べてもらうと、正規分布表の\(x=1.24\) となる面積を求めればよいことが分かります。
数表を使って値を読み取る
手順2で、\(x=1.24\) の値を読み取ればよいことが分かりました。
では、正規分布表を使って読み取っていきましょう。
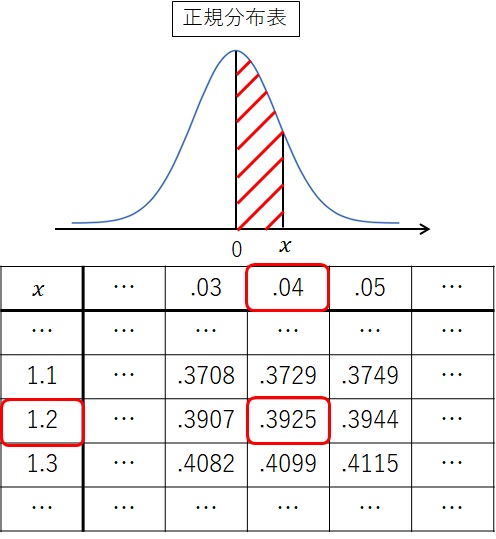
表の一部を抜粋
まずは正規分布表の見方についてです。
表の中に「.3925」など、数字の前に小数点が付いています。これは「0.3925」を表しています。
さて、\(x=1.24\) の読み取り方ですが、\(1.24=1.2+0.04\) と分解します。
上の表を見ると一番左の列に「1.2」という項目があり、一番上の行に「.04」という項目があります。
今回は分かりやすいように赤枠で囲っています。
「1.2」と「.04」が交差する場所に「.3925」と書かれており、この数字が面積になります。
つまり、まとめると、
「\(x=1.24\) となる確率は 0.3925」
となります。
まとめ
本記事では、正規分布表の見方を詳しく解説しました。
表の中には面積の値が書かれており、表の上に描かれているグラフと併せて見ることで、面積を簡単に知ることができます。
表の見方が独特なので、ぜひマスターしましょう。


