周辺確率密度関数とは

同時確率密度関数とは

周辺確率密度関数を考えるときには、同時確率密度関数の知識が前提となっていますので、初めに同時確率密度関数は何かということを説明します。

例題を見てみましょう。

鉄パイプの長さXと重さYが下図のような分布に従うとします。

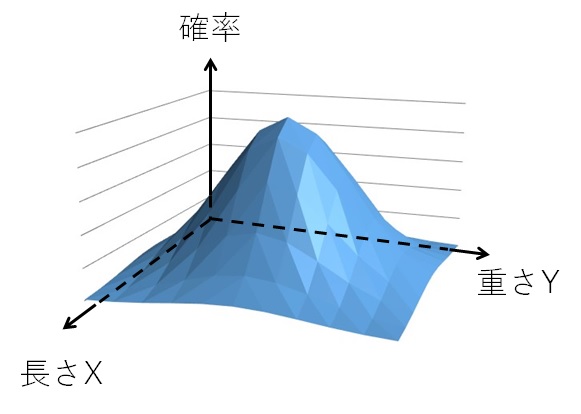
この図は、A君が測定した鉄パイプの長さXと重さYがどのくらいの確率で現れるのかを示しています。
分布の形状のことを同時確率密度関数と呼び、\(f(x,y)\)で表します。
ちなみに、離散型の確率変数の場合は、同時確率関数と呼びます。

また、\(f(x,y)\)は確率密度関数ですので、全区間で積分すると 1 になります。
$$\iint_{S} f(x,y) dxdy=1$$

周辺確率密度関数とは

上記で示しました同時確率密度関数\(f(x,y)\)を使って、周辺確率密度関数は次のように表されます。
$$g(x)=\int_{-\infty}^{\infty} f(x,y) dy$$
$$h(y)=\int_{-\infty}^{\infty} f(x,y) dx$$
\(X\)の周辺確率密度関数を求めるときには \(y\) で積分し、\(Y\)の周辺確率密度関数を求めるときには \(x\) で積分することに注意してください。

周辺確率密度関数は式で書くよりも図を見た方が直感的に理解できると思います。
同時確率と周辺確率の関係を図で表すと、下の図ようになります。

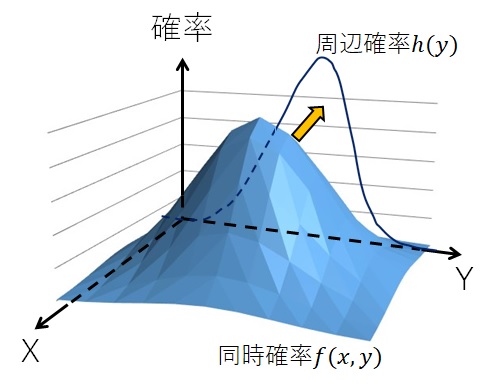
黄色の矢印の\(x\)方向に沿って積分を行うと、\(Y\)の周辺確率密度関数を求めることができます。
\(y\)方向も同様です。

周辺確率密度関数も確率ですので、全区間で積分すると 1 になります。

$$\int_{-\infty}^{\infty} g(x) dx=1$$
$$\int_{-\infty}^{\infty} h(y) dy=1$$

同時確率密度関数と周辺確率密度関数は名称だけ見ると難しそうに感じてしまいますが、表していることは単純です。
筆者は上で示したような図を頭に焼き付けて、忘れないようにしています。