「ヒストグラムの平均値をどうやって求めるか分からない」
「公式に当てはめて計算できることは分かったけど、意味が分からず腑に落ちない」
そう思ったことはありませんか?
応用力をつけるためには、単に公式を覚えるよりも、意味を理解するのが効率的です。
本記事では、ヒストグラムから平均値を求める方法と、その公式の意味を解説しています。
ヒストグラムから平均値を求める手順
次の例題を見ながら、一緒に解いていきましょう。
ある学校の生徒 30 人が国語のテストを受けた。
国語の点数の分布は以下のグラフのようになっていた。
30 人のテストの平均値は?
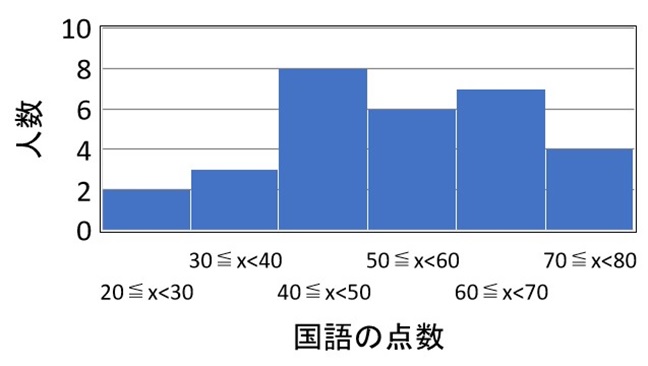
国語の平均点は以下の手順で求めることができます。
1 つ 1 つの区間の中央の値(階級値)を計算する
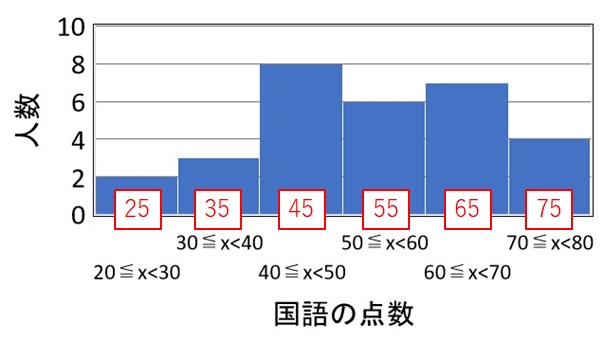
図の赤枠のように、各区間の中央の値を求めて書き込みます。
1 つ 1 つの区間の度数を書き込む
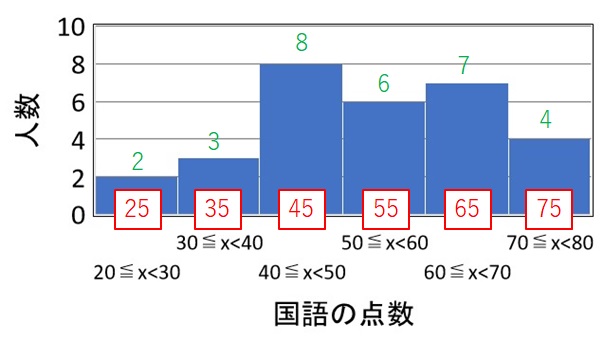
度数とはデータの数のことで、縦軸を見ると分かります。
例題の場合、度数はグラフの中の緑色の数字になります。
手順 1 と手順 2 で求めた値を掛ける
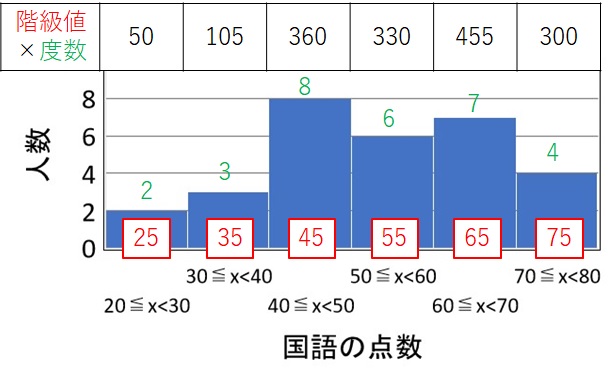
手順 1 で求めた階級値(図中の赤色の値)と、手順 2 で求めた度数(図中の緑色の値)を掛け算します。
掛け算の結果は、グラフの上に書いています。
手順 3 で求めた値を足し合わせて、データの総数で割る
データの総数とは、生徒の人数のことです。
生徒の人数を求めるためには、度数をすべて足し算すれば良いです。
度数の合計は 30 ですので、手順 3 で求めた(階級値)×(度数)をすべて足して、30 で割ります。
$$\frac{50+105+360+330+455+300}{30}=53.3$$
よって、ヒストグラムから求められた平均値は 53.3 点になります。
なお、今までの説明で階級値・度数といった専門用語が出てきました。
これらの意味は別の記事で詳しく説明しています。
また、ヒストグラムから中央値を計算する方法は、次の記事で解説しています。
平均値の求め方の意味
手順 1~4 で平均値を計算することができますが、なぜ平均値が求まるのでしょうか?
実は、あなたがよく知っている平均値の求め方に沿って計算しているのです。
(平均値)=(すべてのデータの合計)÷(データの数)
平均値は上の式のように計算されますので、データの合計と、データの数が分かれば良いです。
それぞれの計算の意味について詳しく見ていきます。
データの合計の求め方
ヒストグラムからでは、各生徒が何点を取ったのか知ることはできません。(区間が「20 ≦ x < 30」のように幅を持っているからです。)
そこで、1 つの区間に含まれる生徒は、全員同じ点数を取ったと考えます。
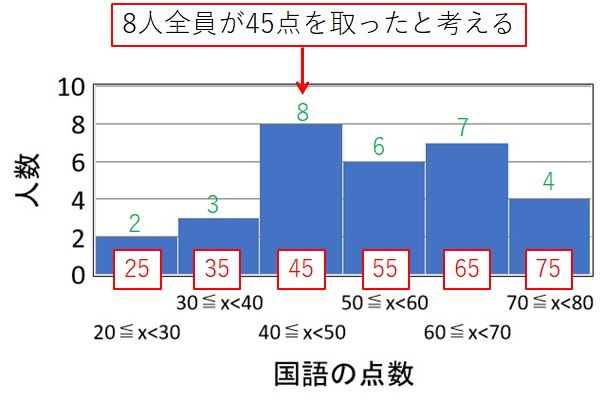
例えば、図のように「40点~50点」を取った 8 人の生徒は、全員 45 点を取ったとします。
このとき、8 人の点数の合計は、
$$45\times 8=360(点)$$
となります。
「45点」=「階級値」、「8 人」=「度数」ですので、すべての区間で
(階級値)×(度数)
を計算して合計すると、全員の点数の合計が計算できます。
データの数の求め方
平均値を計算するためには、データの数も必要です。
ヒストグラムでは、各区間の生徒の数が載っているので、すべて足すとデータの数が求められます。
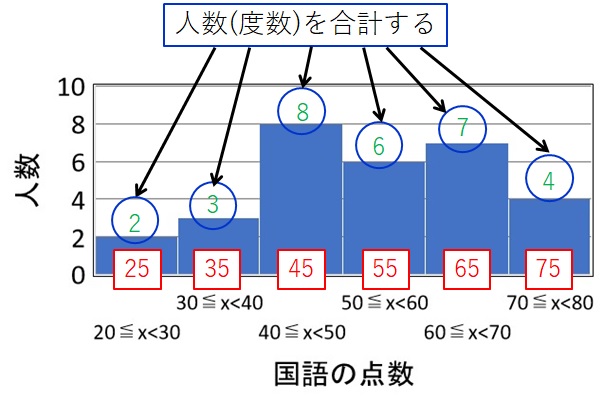
図の青丸で囲った部分が、各区間の生徒の数ですので、これらの数を合計すると、データの数が求まります。
平均値の計算
もう一度、平均値の式を示します。
(平均値)=(すべてのデータの合計)÷(データの数)
おさらいすると、
- データの合計…各区間の生徒全員が同じ点数を取ったと考えて合計する
- データの数…各区間の点数を取った生徒の数を合計する
ヒストグラムから平均値を計算するときには、特別なことは何もしていないことを、お分かりいただけましたでしょうか。
まとめ
本記事では、ヒストグラムの平均値の計算方法と、方法の意味をお伝えしました。
計算手順だけだと覚えにくいですので、平均値を求める理屈を理解するのが近道です。


