確率分布とは？基本概念を理解しよう
確率分布は統計において、とても大切なものです。
「正規分布」「二項分布」などを聞いたことがあるかもしれませんが、これらも確率分布の一種です。
確率分布は統計学特有なので、はじめは考え方が難しく感じるかもしれません。
ですが、確率分布をさけて統計学を理解することはできませんので、一緒にまなんでいきましょう。
確率分布の説明には、「確率変数」が出てきますので、まずはこれを解説します。
確率変数とは？
具体例から入るとわかりやすいので、サイコロを1つ思い浮かべてください。
サイコロの目は1から6までありますが、振ってみるまで、どの目が出るかはわかりません。
みなさんもよく知っているように、サイコロのそれぞれの目が出る確率は1/6です。
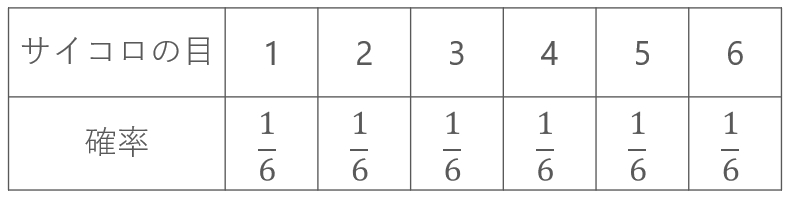
このサイコロの目のように、確率が存在する変数のことを「確率変数」とよびます。
世の中には、たくさんの確率変数の例があります。
- コインの裏表：コインを1回投げたとき、表が出るのと裏が出るのには確率が存在します。
- ATMの利用者数：ATMに1時間内におとずれる利用者数は確率変数と考えることができます。
たとえば、「1人来る確率が0.2」「2人来る確率が0.3」のように考えます。 - 製品の不良品数：工場でつくられた100個の製品のうち、不良品となる数は確率変数です。
たとえば「3個不良品となる確率が0.1」と考えます。
例を見てわかるように、一見確率とは何の関係もなさそうなものでも、値に確率を対応させることで、確率変数とみなすことができます。
確率分布とは？
確率分布は、「確率変数と、その確率全体をあらわしたもの」です。
つまり、先ほど示した、サイコロの出る目の確率表は、確率分布です。
もう少し説明すると、サイコロの出る目が「確率変数」で、上の表全体のことを「確率分布」とよびます。
他の例もみてみます。
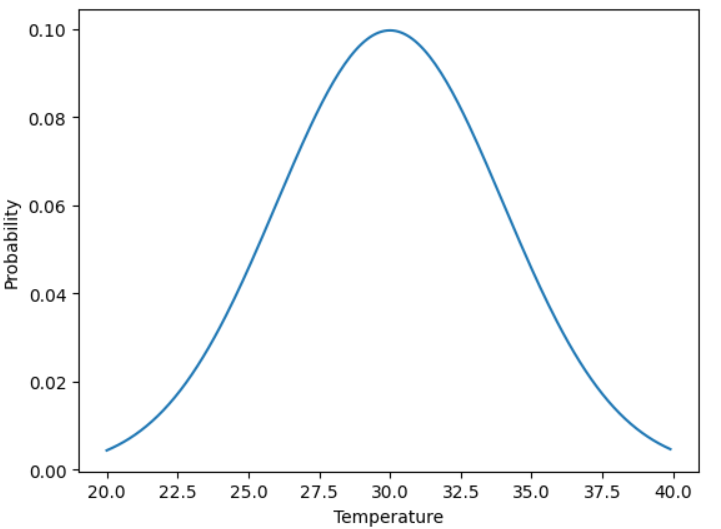
ある都市の1日の平均気温を考えます。
「28度から29度の気温になる確率が0.1」のように考えると、平均気温は確率変数です。
そして、確率変数（=平均気温）に対する確率をまとめたグラフが確率分布になります。
確率分布は大きく2つにわけられます。
それは、離散型確率分布と連続型確率分布です。
「離散」というのは確率変数がとびとびのことで、サイコロの出る目は離散です。
「連続」というのは確率変数が連続的な値をとるもので、先ほどの平均気温の例は連続です。
これらはグラフを見ると違いが一目でわかります。
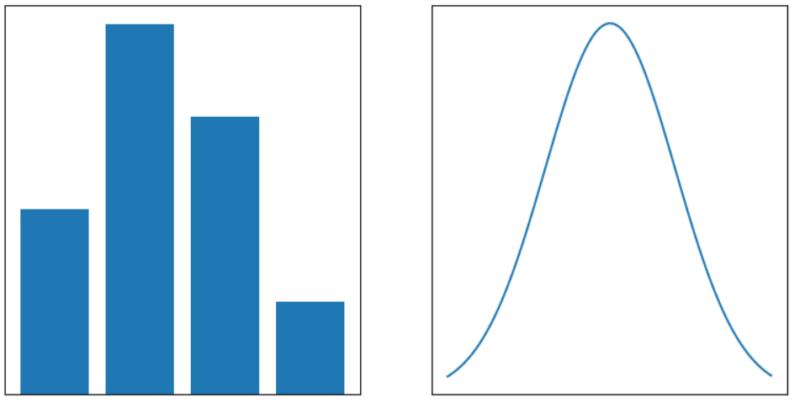
左のグラフが離散型確率分布で、右のグラフが連続型確率分布です。
代表的な離散型確率分布
離散型確率分布として、代表的な「二項分布」「ポアソン分布」を紹介します。
二項分布
ある工場の製品検査では、確率0.2で不良品がでる。
この工場から製品を5個とったとき、その中で不良品がそれぞれ1、2、3、4、5個である確率はどのくらいか。
二項分布は、確率pで「成功」か「失敗」のどちらかに分類できる問題につかうことができます。
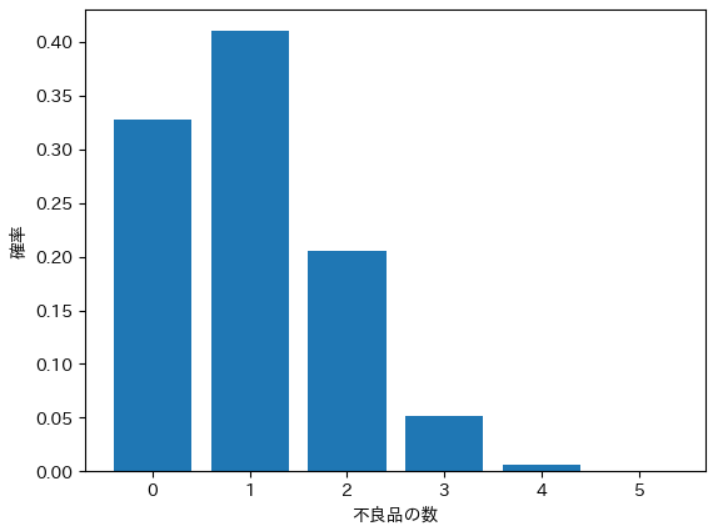
例題は二項分布を使うことができて、計算すると次のグラフのようになります。
確率0.2ということは、5個あれば、だいたい1個が不良品ということなので、グラフでも1付近の確率が高くなっています。
ポアソン分布
あるコールセンターでは、1時間あたり平均で3件の電話がかかってきます。
このとき、1時間で電話がそれぞれ0件、1件、・・・、10件かかってくる確率はどのくらいか。
ポアソン分布は、一定の時間に発生する回数をあらわします。
例題のように、一定時間で平均どのくらい発生するかがわかれば、確率分布をつくることができます。
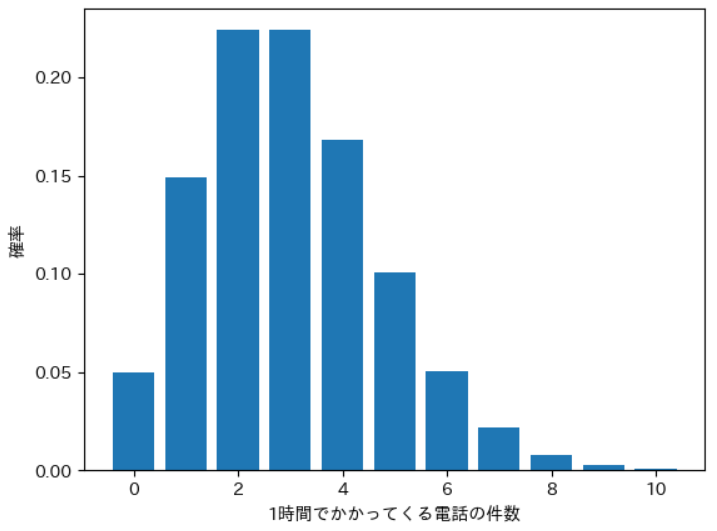
実際に計算してみた結果は下図のようになります。
平均3件かかってくるので、3付近の確率が高くなっているのがわかります。
代表的な連続型確率分布
続いて、連続型確率分布として有名な「正規分布」「指数分布」を紹介します。
正規分布
あるクラスで数学のテスト（満点100点）がおこなわれました。
平均点は70点、標準偏差（データの広がり具合をあらわす数値）が10点です。
60点から80点の間にいる生徒はどれくらいいますか。
正規分布は統計学でいちばん有名な分布です。つりがねの形をしています。
例題をグラフで描くと下図のようになります。
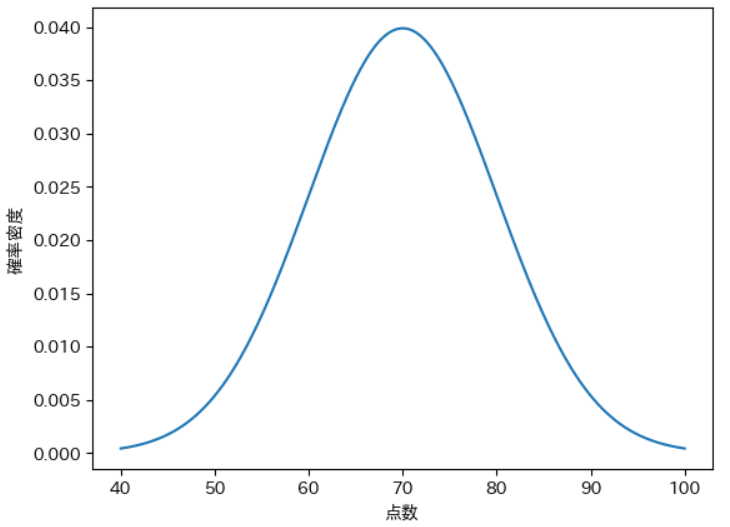
連続型確率分布では、縦軸が「確率密度」という値になります。
これは、特定の範囲内にデータが存在する可能性をあらわしています。
たとえば、例題では、「60点から80点の間にいる生徒はどのくらいか」という問題でした。
60点から80点の間の面積が確率をあらわし、計算するとだいたい68%となります。
指数分布
あるバス停では、バスが平均して10分ごとに到着します。
バスの到着間隔はランダムです。
次のバスが5分以内に到着する確率はどのくらいか。
指数分布は、一定の発生確率でおこるイベントの時間間隔をあらわします。
バスの待ち時間だけでなく、部品が故障するまでの時間や、顧客が次に来店するまでの時間にも応用できます。
この例題をグラフにすると次のようになります。
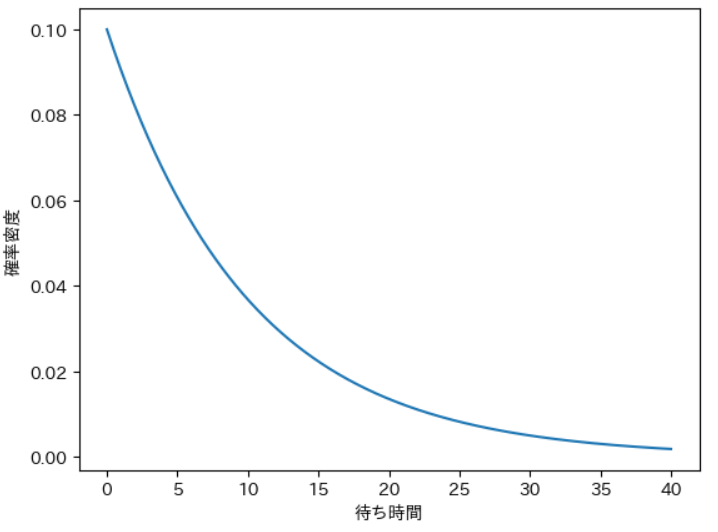
次のバスが5分以内に到着する確率は、グラフの面積を計算して、だいたい39%になります。
確率分布の応用例
確率分布がビジネスでどのように利用されるか、いくつか具体例をあげます。
自動車保険では、1年間に発生する交通事故件数をポアソン分布で予測して、それにもとづいて保険料を計算することができます。
製造ラインでは、不良品数を二項分布で予測して、品質基準を設定することができます。
コールセンターでは、電話がかかってくる時間間隔を指数分布で予測して、効率的な人員配置を考えることができます。
以上のように、ビジネスでは何らかの値（交通事故件数、不良品数、電話の到着間隔など）を確率分布にあてはめることで、さまざまな意思決定ができます。
確率分布など数学の計算ができるようにすることを「モデル化」といいます。
モデル化することで、どのくらい事故がおこるか、どのくらい不良品が発生するか、どのくらい電話がかかってくるか予測できて、対策が立てやすくなります。
統計学の強みは、どのくらいの確率で発生するか計算できるので、発生原因はわからなくても、対策を立てられることにあります。
まとめ
本記事では、確率分布の基本と応用例について解説しました。
確率分布を構成しているものは、確率変数と確率です。
確率変数とは、確率をわりあてることのできる変数です。
確率変数と確率をセットにして、それらをまとめたものが確率分布です。
確率分布には、離散型確率分布と連続型確率分布があります。
離散型確率分布として、「二項分布」「ポアソン分布」を紹介しました。
連続型確率分布として、「正規分布」「指数分布」を紹介しました。
ビジネスでは、現象をモデル化して確率分布にあてはめることで、さまざまな予測ならびに意思決定が可能になります。
