共分散とは
2つの確率変数\(X\)と\(Y\)の関係性を表すのが共分散です。
共分散は以下のように定義されます。
$$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]$$
上の式において、\(Cov(X,Y)\)が\(X\)と\(Y\)の共分散、\(E[X]\)は\(X\)の期待値を表します。
共分散は分散と違って、正の値も負の値も取り、およそ次のような関係があります。
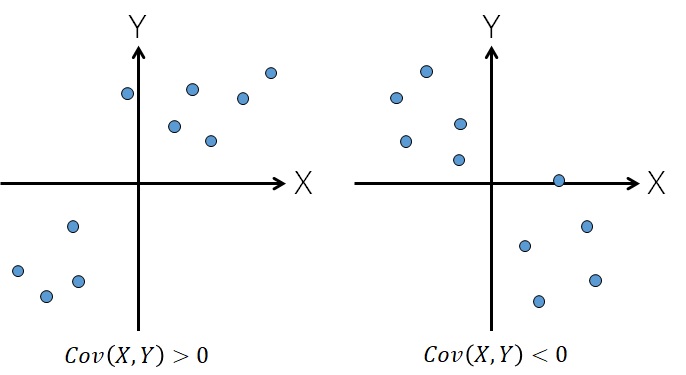
左図のように、\(X\)が大きくなると\(Y\)も大きくなるときに正の値を取り、\(X\)が大きくなると\(Y\)が小さくなるときに負の値を取ります。
ただし、\(X\)と\(Y\)の傾向の強さを共分散の値から判断することはできません。
(\(X\)と\(Y\)の傾向の強さを判断できるようにしたものが相関係数です)
共分散の性質
共分散の計算において重要な性質は主に次の3つです。
以下の式において、\(Cov(X,Y)\)が共分散、\(E(X)\)が期待値、\(V(X)\)が分散です。
\begin{align}
&(1)V(X+Y)=V(X)+V(Y)+2Cov(X,Y)\\
&(2)a,b,c,dを定数とするとき\\
& Cov(aX+b,cY+d)=ac Cov(X,Y)\\
&(3)Cov(X,Y)=E(XY)-E(X)E(Y)
\end{align}
(1)は\(X\)と\(Y\)の加法の分散は、単純な分散の加法とならないことに注意すべき式です。
(3)は共分散を期待値だけで表したもので、共分散の定義から直接計算するよりも(3)を使って計算する方が楽に計算できることもあります。
次の節で(1)~(3)を証明していきます。
共分散の性質の証明
(1)~(3)を順に証明します。
証明の中で、「期待値の性質」と書かれている部分は、リンク内の性質を使っています。
様々な種類の括弧を使っているので複雑ですが、括弧がどの部分を囲っているのかに注意しながら読み進めてください。
$$(1)V(X+Y)=V(X)+V(Y)+2Cov(X,Y)$$
\begin{align}
(1)V(X+Y)&=E[(X+Y-E(X+Y))^2] ←分散の定義\\
&=E[(X+Y-E(X)-E(Y))^2] ←期待値の性質\\
&=E[((X-E[X])+(Y-E[Y]))^2]\\
&=E[(X-E[X])^2+(Y-E[Y])^2+2(X-E[X])(Y-E[Y])]\\
&=E[(X-E[X])^2]+E[(Y-E[Y])^2]+2E[(X-E[X])(Y-E[Y])] ←期待値の性質\\
&=V(X)+V(Y)+2Cov(X,Y)
\end{align}
(1)では、計算量を少なくするために、2乗を展開するまでの準備がポイントとなります。
$$(2)Cov(aX+b,cY+d)=ac Cov(X,Y)$$
\begin{align}
(2)Cov(aX+b,cY+d)&=E[(aX+b-E[aX+b])(cY+d-E[cY+d])]\\
&=E[(aX+b-aE[X]+b)(cY+d-cE[Y]+d)] ←期待値の性質\\
&=E[a(X-E[X])c(Y-E[Y])]\\
&=ac E[(X-E[X])(Y-E[Y])] ←期待値の性質\\
&=ac Cov(X,Y)
\end{align}
(2)では、初めに\(E[aX+b]\)と\(E[cY+d]\)を展開しています。
$$(3)Cov(X,Y)=E(XY)-E(X)E(Y)$$
\begin{align}
(3)Cov(X,Y)&=E[(X-E[X])(Y-E[Y])]\\
&=E[XY-X\cdot E(Y)-Y\cdot E(X)+E(X)E(Y)]\\
&=E(XY)-E(X)E(Y)-E(Y)E(X)+E(X)E(Y) ←期待値の性質\\
&=E(XY)-E(X)E(Y)
\end{align}
(3)は初めに\(E[\cdot]\)の中を展開しています。
2行目から3行目の変形で、2行目の式の中にある\(E(X)\)と\(E(Y)\)は定数であることを利用しています。
以上、式が長くなってしまいましたが、共分散の性質が証明されました。
見た目の印象では難しそうに見えますが、式の展開と期待値の線形性を繰り返し用いているのみです。
共分散の性質のみならず、期待値の性質を理解する良い練習ですので、紙に書いてみましょう。


