ベイズの定理を使う例題【病気にかかっている確率とモンティホール問題】

ベイズの定理ってどうやって使うの？
記号ばっかりで、公式を覚えても問題が解けない…

本記事では、ベイズの定理を具体的に使う方法を解説します。
例題を２つ用意しました。

病気にかかっている確率
モンティホール問題

どちらも有名な問題で、ベイズの定理を知らないとまちがえてしまいます。
例題にベイズの定理を当てはめる方法を詳しく説明します。

ベイズの定理の公式
例題１　病気にかかっている確率
例題２　モンティホール問題
まとめ

ベイズの定理の公式

ベイズの定理は結果がわかったときに、原因を求める確率を計算することができます。
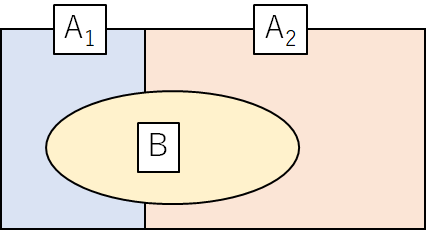
$B$ が結果で、$B$ の原因として $A_1$、$A_2$ の２つが考えられるとき、
$A_1$ が原因である確率は、以下の式で求めることができます。
$$P(A_1|B)=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}$$
原因と結果の関係を図で表すと、以下のようになります。

ベイズの定理の証明や、定理のイメージを理解したい方は、以下の記事をご覧ください。

ベイズの定理をわかりやすく解説！【証明を直感で理解する】

ベイズの定理って何？記号ばっかりで覚えられる気がしない… ベイズの定理を見たとき、式の複雑さに圧倒されていませんか？本記事では、ベイズの定理の意味を図で詳しく解説します。はじめにベイズの定理の証明を示します。証明では数式が多くなってしまいま...

さて、本記事ではベイズの定理の使い方を、２つの例題で見てみます。

例題１　病気にかかっている確率

病気にかかっている確率を求める問題は、ベイズの定理を使う問題として非常に有名ですので、解法は覚えてしまうくらいが良いです。

例題

日本の人口のうち、1%が病気Aにかかっている。

病気Aにかかっている人のうち、90%が陽性と診断され、
病気Aでない人のうち、5%が陽性と診断される。

タロウ君が病気Aにかかっているか知るために検査を受けたところ、陽性と診断された。

タロウ君が病気Aにかかっている確率を求めよ。

病気Aにかかっている人のうち、90%が陽性だから、

タロウ君が病気Aにかかっている確率は90%

直感的には 90% と思ってしまいますが、実は 90% ではありません。

なぜなら、病気Aにかかっている人は日本全体の 1% しかいないからです。

図を見ていただくと分かるように、病気Aでない人が圧倒的に多いので、
まちがって陽性と診断される(偽陽性)影響が無視できないからです。

ベイズの定理を使って解くのが正しいやり方になります。

病気Aにかかっている確率を $P(A_1)$、病気Aでない確率を$P(A_2)$、陽性と診断される確率を $P(B)$ とおくと、問題文から以下の確率が分かります。

$P(A_1)=0.01$…病気Aにかかっている人が人口の 1%
$P(B|A_1)=0.9$…病気Aにかかっている人のうち、陽性になる確率は 90%
$P(B|A_2)=0.05$…病気Aでない人のうち、陽性になる確率は 5%

ベイズの定理の式に当てはめると解くことができます。
\begin{align}
P(A_1|B)&=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}\\
&=\frac{0.9\times 0.01}{0.9\times 0.01+0.05\times 0.99}\\
&=0.15
\end{align}
結果は 15% です。陽性と診断されたのに、実際に病気Aにかかっている確率は小さいと思いませんか？

陽性と診断されたからといって病気Aにかかったと決めつけるのではなく、冷静に判断することが大切です。

病気にかかっている確率の問題は、人間の直感と反するので、まちがえやすいです。

例題２　モンティホール問題

モンティホール問題も病気にかかる確率と同じく、人間の直感に反する問題です。

例題

宝箱が３つあり、どれか１つに宝石が入っている。

2人が挑戦者と司会者に分かれ、挑戦者が宝石の入った宝箱を当てる。
司会者は、どれが宝石の入った宝箱かを知っている。

次の手順でゲームを行う。

３つの宝箱から、挑戦者が適当に宝箱を１つ選ぶ
司会者は残った宝箱のうち、空箱を開ける
ただし、両方とも空箱の場合は、どちらかをランダムに開ける
挑戦者はえらんだ宝箱を変更することができる

挑戦者は宝箱を変更する方が良いかどうか答えよ。

問題の状況設定がややこしいので、図を使って整理します。

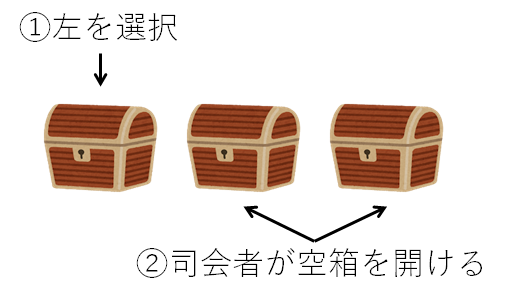
たとえば、挑戦者が左の宝箱を選んだとします。
残った宝箱のうち、司会者は空の宝箱をオープンします。

たとえば、司会者が右の宝箱をオープンしたら、挑戦者は残った方の宝箱のどちらかを、もう一度えらび直すことができるということです。

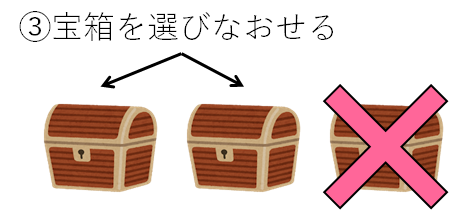
最初にえらんだ宝箱を変更した方が良いのでしょうか？
ちょっと考えてみましょう。

…

…

答えは決まりましたでしょうか？
正解は「宝箱を変更した方がよい」です。

え？

宝石はランダムに入れられてるから両方とも 50% じゃないの？

と思いますよね。私もはじめてモンティホール問題を解いたときは、同じように思いました。

両方とも 50% でない理由は、「同様に確からしくない」からです。

たとえば、最初に左の宝箱を選んだとき、左に宝石が入っている確率は 1/3 です。

司会者が中央の宝箱を開けても、右の宝箱を開けても、左に宝石が入っている確率は 1/3 で変わりません。

司会者が宝箱を開けたあとでは、宝箱は２つしか残っていませんから、宝箱を変更すると、確率は
$$1-\frac{1}{3}=\frac{2}{3}$$
となるのです。

…まだ納得できませんか？

ベイズの定理を使って確認してみましょう。

最初に左の宝箱を選んで、司会者が右の宝箱を開けたとします。
このとき、宝石が入っているのは、左または中央です。

$P(A_1)$…左の宝箱に宝石が入っている確率
$P(A_2)$…中央の宝箱に宝石が入っている確率
$B$…司会者が右の宝箱を開けたという情報

ベイズの定理にあてはめると、司会者が右の宝箱を開けたときに、左の宝箱に宝石が入っている確率は、
\begin{align}
P(A_1|B)&=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}\\
&=\frac{\frac{1}{2}\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+1\times \frac{1}{3}}\\
&=\frac{1}{3}
\end{align}
司会者が右の宝箱を開けたときに、中央の宝箱に宝石が入っている確率は、
\begin{align}
P(A_2|B)&=\frac{P(B|A_2)P(A_2)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}\\
&=\frac{1\times \frac{1}{3}}{\frac{1}{2}\times \frac{1}{3}+1\times \frac{1}{3}}\\
&=\frac{2}{3}
\end{align}
となって、宝箱を変更するほうが当たる確率が高くなります。

モンティホール問題は一度見たことがないと、まちがった答えを出してしまいます。