線形回帰とは何が違う?ロジスティック回帰とは
ロジスティック回帰とは、「メールがスパムかどうか」「商品が不良品かどうか」「顧客が商品を買ってくれるかどうか」など、0か1かを判断するモデルです。
これらは二値分類とよばれていて、ロジスティック回帰は二値分類の問題を解くときに使われています。
似たようなモデルに線形回帰がありますが、次のような違いがあります。
- 線形回帰:「住宅価格を予測する」など連続的な数値を予測するのに使われる
- ロジスティック回帰:「購入するかしないか」など二値の分類問題に使われる
また、ロジスティック回帰の特徴として、出力が0から1の範囲の数値となります。確率として解釈することができ、たとえば、ある顧客が商品を購入する確率が0.8であれば、「80%の確率で購入する」と解釈できます。
ロジスティック回帰は医療分野での疾患リスク予測や、マーケティング分野での顧客行動分析など、多くの実務領域で利用されています。
シンプルで解釈しやすいので、データ分析を専門としていない人でも扱いやすいです。
具体例からまなぶロジスティック回帰の使い方
ロジスティック回帰を使った例を解説します。
サブスクリプション型サービス(動画配信や音楽ストリーミングなど)で、ユーザーがサービスを継続するか解約するかを予測してみます。
月間視聴時間と最終利用からの日数データをとったところ、次の表のようになりました。
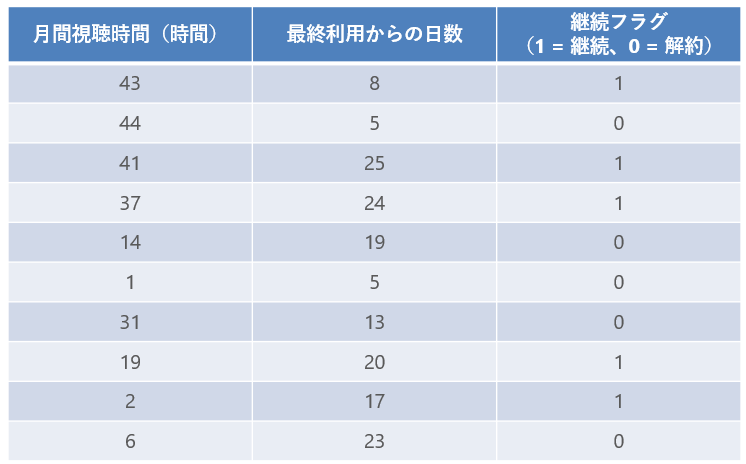
目的は、月間視聴時間と最終利用からの日数がどのくらいであれば、継続する確率がどのくらいになるのかを知ることです。
データに対してロジスティック回帰を適用すると以下のようになります。

なんでロジスティック回帰がこのような数式になっているのか、については後ほど説明します。
これで継続する確率を数式であらわすことができたので、予測が可能になります。
たとえば、視聴時間が20時間、最終利用からの日数が10日のユーザーがいた場合、そのユーザーのサービス継続率は0.235(23.5%)と求めることができます。
この具体例からわかるように、モデルを構築すると、説明変数(視聴時間、最終利用からの日数)から確率値を出せるようになるので、意思決定をサポートできます。
オッズとロジスティック回帰の数式の仕組み
前節では、ロジスティック回帰を使って、サービス継続確率を求めました。
そのときに見慣れない数式が出てきたので、ここでは数式の仕組みを解説します。
まず、ロジスティック回帰を作るときに最初に思いつくのは、「0と1を判断する二値分類の問題において、1となる確率を線形回帰であらわしたい」となります。
つまり、式で書くと次のようになります。
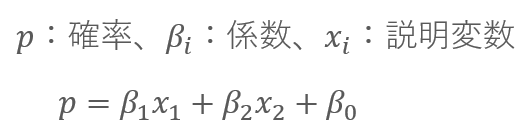
たとえば、前節のサービス継続確率モデルであれば、「視聴時間と最終利用からの日数から、サービス継続確率を求める」です。
しかし、この式には致命的な欠陥があります。
それは、確率は0から1までの値をとるのに対して、線形回帰は無限大までの値をとるので、数式が成り立たなくなることです。
この欠陥を解消するために「オッズ」というものを導入します。
オッズは競馬で聞いたことがあるかもしれませんが、統計学としての意味を解説します。
たとえば、商品を購入した人が60人、購入しなかった人が40人いたとします。
直感的にわかるように、この商品の人気のオッズは1.5倍になります。
なぜなら、「商品がえらばれる確率(0.6)」と「商品が選ばれなかった確率(0.4)」の比が1.5だからです。
このことを数式としてあらわすと以下のようになります。

オッズは無限大までの値をとるので、確率の代わりに使えそうです。
実際にロジスティック回帰に使うときには、数学的な理由からオッズの対数(ロジットとよぶ)を利用します。
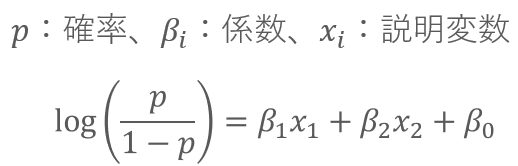
上式がロジスティック回帰の式です。
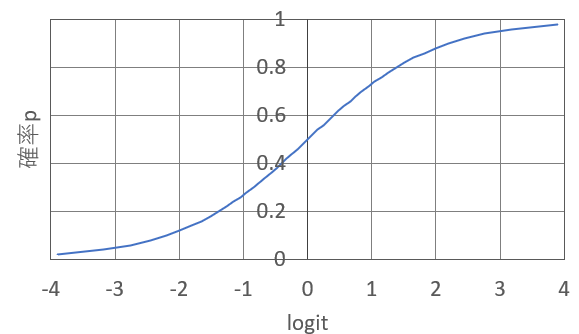
横軸にロジット、縦軸に確率をとると以下のようなグラフになります。
つまり、ロジスティック回帰の右辺(=ロジット)が0付近では確率が大きく変化して、0から離れるほど確率の変化はゆるやかになります。
係数を解釈できるオッズ比とは
ロジスティック回帰の魅力のひとつは、モデルの係数を「オッズ比」として解釈できることです。
オッズ比は説明変数がどのくらいの影響を与えているのかを直感的に理解することができます。
具体例がわかりやすいので、先ほど使った「視聴時間と最終利用からの日数をつかって、サービス継続確率を求めるモデル」を再掲します。

このモデルで、「視聴時間はサービス継続確率にどのくらいの影響をあたえているのか」をみてみます。
オッズ比は係数を指数関数で変換すると計算できます。
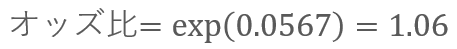
オッズ比の解釈方法は、「視聴時間が1時間増えたら、サービス継続の可能性(オッズ)は約6%増加する」です。
つまり、オッズ比は、説明変数の値が1だけ増えたときに、オッズがどのくらい変わるのか、ということを表します。
オッズとは、イベントが起こる確率と、起こらない確率の比です。
たとえば、サービス継続確率が60%(0.6)のとき、オッズは、
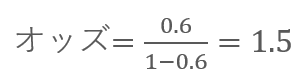
この場合、「継続する可能性は継続しない可能性の1.5倍」と解釈できます。
オッズ比が、係数の指数関数となる理由を証明します。

以上の式から、「説明変数の値が1ふえると、オッズの変化率は、係数の指数関数にひとしい」ことが証明できました。
ロジスティック回帰のモデル自体の評価をするには、ROC曲線というものを使います。
ROC曲線は次の記事で扱っています。
まとめ
ロジスティック回帰は、二値分類をモデル化します。
モデルの出力を確率として解釈することができ、たとえば、ある顧客が商品を購入する確率が0.8であれば、「80%の確率で購入する」と解釈できます。
ロジスティック回帰の数式はオッズを使って構築されています。
オッズとは、たとえば、「商品がえらばれる確率(0.6)」と「商品が選ばれなかった確率(0.4)」があったときに、「商品がえらばれる可能性は、えらばれない可能性の1.5倍」と解釈できます。
ロジスティック回帰の係数を解釈するには、オッズ比を使えばよく、オッズ比を求めることで、「視聴時間が1時間増えたら、サービス継続の可能性(オッズ)は約6%増加する」のように解釈することができます。