ROC曲線の基礎
ROC曲線とは、機械学習の二値分類の良さをグラフで表したものです。
二値分類とは、病気にかかっているか、製品が不良品かどうか、など0または1に分類できる問題のことです。
二値分類モデルとしては、ロジスティック回帰が有名で、次の記事で解説しています。
実際にROC曲線の例を下に描いてみました。
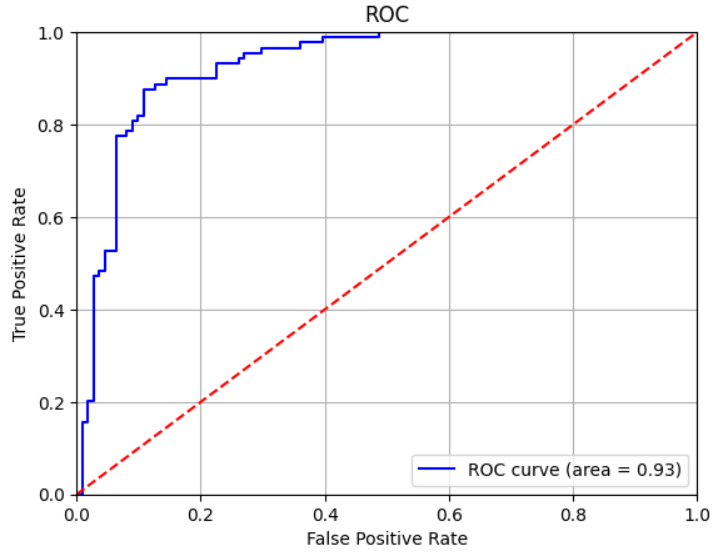
グラフの横軸は偽陽性率(FPR: False Positive Rate)、縦軸は真陽性率(TPR: True Positive Rate)です。
真陽性率(TPR)とは、本当に(True)陽性(Positive)であった割合(Rate)のことです。
つまり、Positiveのものを正しくPositiveと判定できた割合を指します。
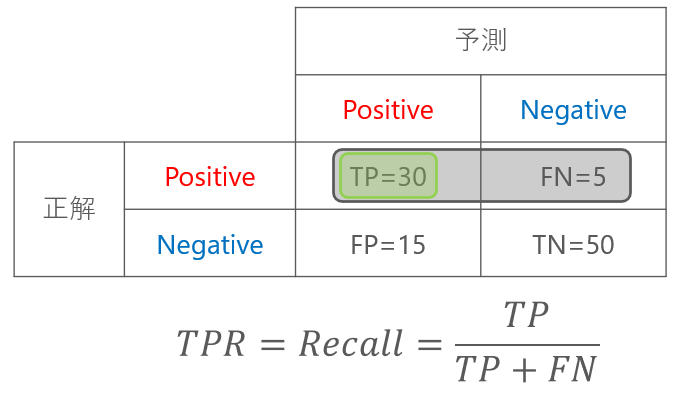
混同行列で表すと上図のようになります。TPRは再現率(Recall)と同じ計算式になります。
次に偽陽性率(FPR)とは、間違えて(False)陽性(Positive)と判定した割合(Rate)のことです。
つまり、本当はNegativeであるにも関わらず、Positiveと予測してしまった割合を指します。
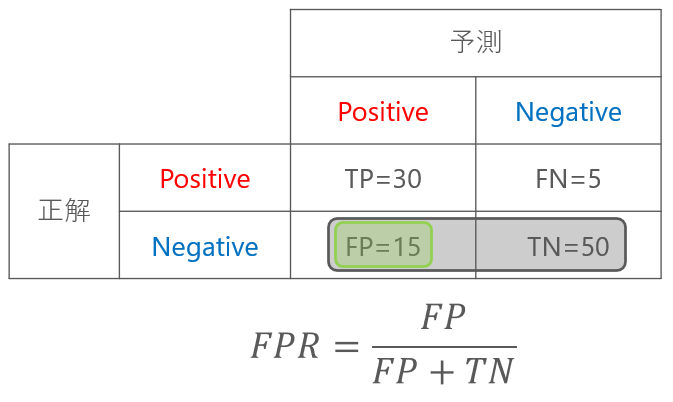
混同行列では上図のようになります。TPRとFPRを見比べていただくと違いがわかりやすいと思います。
今まで見てきたように、ROC曲線の意味を理解するには混同行列の知識がいります。
混同行列がよくわからない方は、下の記事で解説しているので参考にしてください。
ROC曲線を直感的に理解する
ROC曲線をイメージ図を使って説明します。
ROC曲線は二値分類で使われるので、ラベル0の分布とラベル1の分布というものを考えます。
ラベル0とラベル1の分布のイメージを描くと以下のようになります。
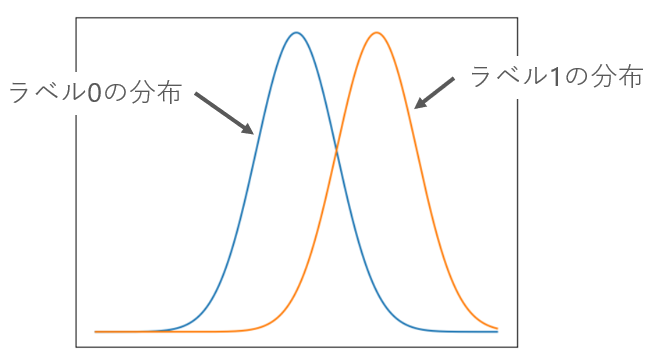
ROC曲線を描くときには「閾値(しきいち)」という考え方を使います。モデルの予測確率が閾値以上であればラベル1と見なす、という考え方です。
閾値を付け足した図を示します。
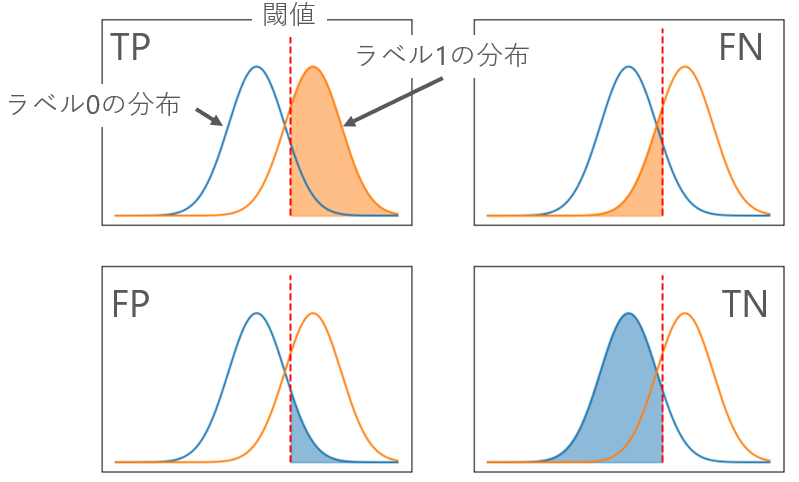
閾値以上をラベル1、以下をラベル0と見なすので、たとえば左上の図では、実際にラベル1で正しくラベル1と予測できている部分(TP: True Positive)をあらわしています。
他の図についても同じことがいえます。
閾値をひくことで、TP、FN、FP、TNが計算できるので、ROCのグラフに点を打つことができます。
この閾値を動かすことで、グラフに次々と点を打つことができてROC曲線が完成します。
次節で実際にROC曲線を描いてみます。
ROC曲線のつくり方
プログラムを使うと中身がブラックボックスとなりがちなので、手でROC曲線を描いてみます。
以下のようなデータがあるとします。

予測確率は機械学習モデルが出力した値で、確率が高いほど「ラベル1」である可能性が高いと予測しています。
さて、この表からROC曲線を描いてみます。
ROC曲線を作るときには「閾値」が必要です。
たとえば閾値を0.6に設定すると、モデルの予測確率が0.6以上のデータはラベル1、0.6未満のデータはラベル0とする、ということです。
閾値を導入することで予測確率を混同行列に変換することができ、ROC曲線を描くことができます。
実際に、閾値を0.6とした場合の結果を下に示します。
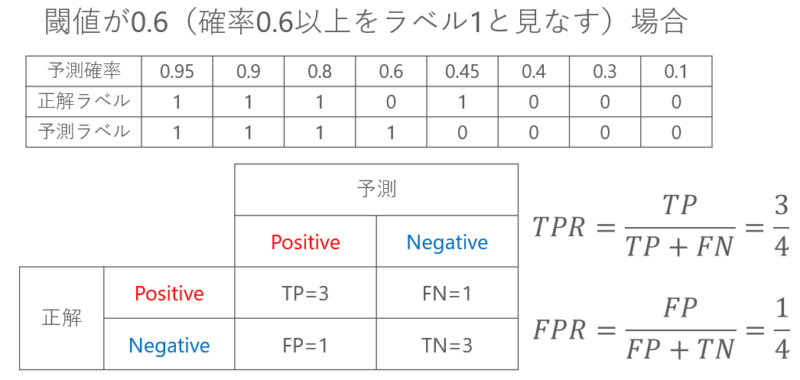
上図には、予測確率・正解ラベルの他に、予測ラベルという行を追加しています。閾値が0.6なので、0.6以上をラベル1として書いています。
正解ラベルと予測ラベルを見ることで、混同行列を上図のように書くことができて、TPRとFPRを計算することができます。
ROC曲線は、閾値を変えながらTPRとFPRを計算して、それらをプロットしたものです。実際にプロットすると以下のようになります。
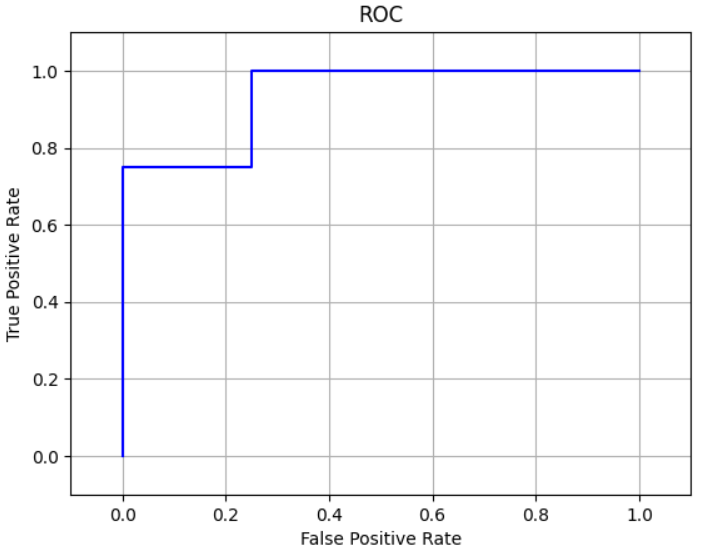
閾値0.6のときはTPR=3/4=0.75、FPR=1/4=0.25だったので、この点を通っていることがわかります。
AUCの意味と読み方
前節まででROC曲線を描くことはできましたが、この曲線をどのように解釈したらよいのでしょうか。
ROC曲線を解釈するための指標として、AUC(Area Under the Curve)があります。
その名の通り、曲線の下の面積のことです。

この曲線の場合にはAUC=0.93となっています。
一般的に、AUCの数値が高ければ高いほど、モデルの分類性能は高いです。
AUCの評価基準は一般的に次のようになります。
- AUC = 1.0:理想的なモデルで、すべての陽性(ラベル1)と陰性(ラベル0)を完全に区別できている。
- AUC = 0.5:完全にランダムで、まったく分類できていない。
- AUC < 0.5:陽性と陰性が逆になっている可能性があり、モデルの見直しが必要。
基本的にはAUCの値は0.5から1.0の間になり、0.8~0.9以上あれば精度は高いといえます。
まとめ
本記事では、二値分類の評価として重要なROC曲線とAUCについて解説しました。
ROC曲線の縦軸と横軸は、それぞれ次のような意味をもっています。
- 縦軸はTPR:Positiveのものを正しくPositiveと判定できた割合
- 横軸はFPR:本当はNegativeであるにも関わらず、Positiveと予測してしまった割合
ROC曲線を描くときには閾値という考え方を持ち込みます。
モデルの予測確率が閾値以上であればラベル1と見なす、という考え方です。
閾値を動かしながらTPRとFPRを計算するとROC曲線を描くことができます。
ROC曲線の下の面積をAUCとよび、AUCは0から1の値をとります。
AUC = 0.5のときは完全ランダムな予測で、AUC = 1.0は完璧に分類できている予測です。
AUCは分類モデルの性能をひとつの数値であらわすことができるので便利です。