混同行列とは
混同行列(Confusion Matrix)は、機械学習の二値分類の性能をはかるために使われます。
二値分類とは、Yes/Noで表すことのできる問題で、ビジネスでは下記のような例があります。
- 医療診断で、病気にかかっているかどうかを表す
- メールがスパムかどうか判定する
- 工場で生産された品物が不良品かどうか判定する
- 金融取引で詐欺かどうか見分ける
二値分類ができる代表的なモデルとして、ロジスティック回帰があります。
ロジスティック回帰については以下の記事で取り扱っています。
なぜ二値分類の性能評価が必要かというと、機械学習はまちがえることがあるからです。
どのくらい正しく分類できたのかを数値であらわすために混同行列を使います。
TP・TN・FP・FNの覚え方
さっそくですが、混同行列を見てみましょう。
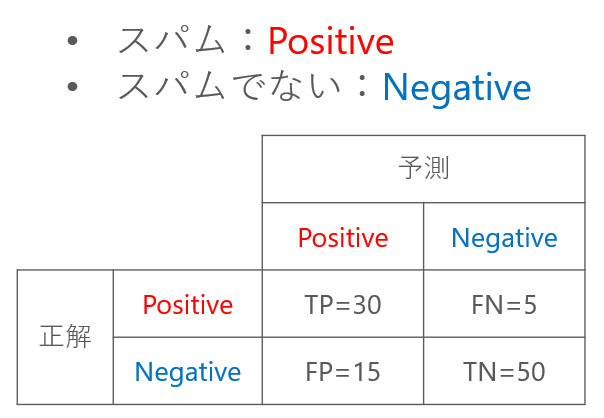
例として、メールがスパムであるかどうかを判定した結果を出します。
Positive/Negativeは日本語では陽性/陰性と書かれることが多いですが、それだと病気の判定のイメージがついてしまうので、本記事では英語のまま説明します。
Positiveは問題があると考えられるクラスで、医療診断なら病気である、不良品判定では不良品である、金融取引判定では詐欺取引である、ことを表します。
Negativeは問題がない通常のクラスです。
表の見方を説明します。
- TP (True Positive):「スパムメール」を、正しく「スパム」と判定できた
- FP (False Positive):「スパムメールでないもの」を、まちがって「スパム」と判定した
- FN (False Negative):「スパムメール」を、まちがって「スパムでない」と判定した
- TN (True Negative):「スパムメールでないもの」を、正しく「スパムでない」と判定した
そのままだと、かなり覚えにくいので、以下のように覚えるといいです。
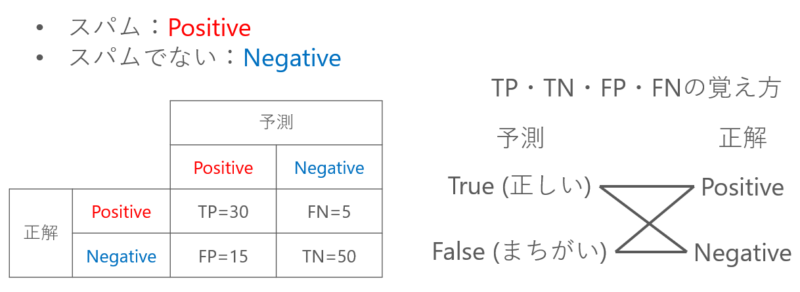
つまり、
- True/Falseは予測が合っているか、まちがっているか
- Positive/Negativeは正解ラベルがYesかNoか
となります。これを踏まえて、もう一度混同行列を見てみます。
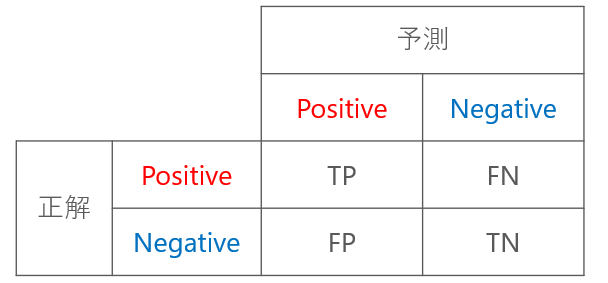
- TP (True Positive):予測は正しくて、正解ラベルはPositive
- FP (False Positive):予測はまちがっていて、正解ラベルはPositive
- FN (False Negative):予測はまちがっていて、正解ラベルはNegative
- TN (True Negative):予測は正しくて、正解ラベルはNegative
このようにすると、覚えやすくなります。
混同行列だけでは読み取るのが大変なので、分類の良しあしをはかる指標を次の節から紹介します。
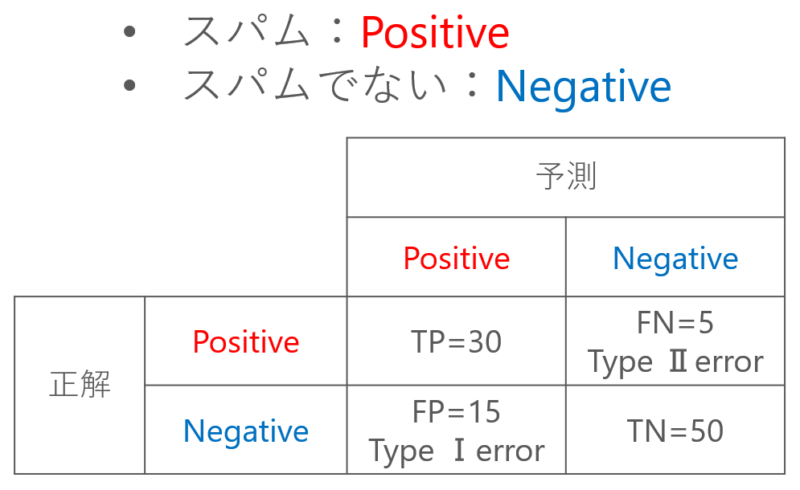
統計学の専門用語で、以下の用語があります。
- 第一種の過誤:帰無仮説が正しいときに、棄却する誤り
- 第二種の過誤:帰無仮説がまちがっているときに、採択する誤り
False Positiveは、実際にはNegativeであるものを、Positiveと判定してしまったので第一種の過誤です。
False Negativeは、実際にはPositiveであるものを、Negativeと判定してしまったので第二種の過誤です。
つまり、混同行列の中に書くことができます。
正解率(Accuracy)
正解率とは読んで字のごとく、どのくらい正しく予測できたかを表します。
計算式は、全体に対する正しく予測できた(TP・TN)割合です。
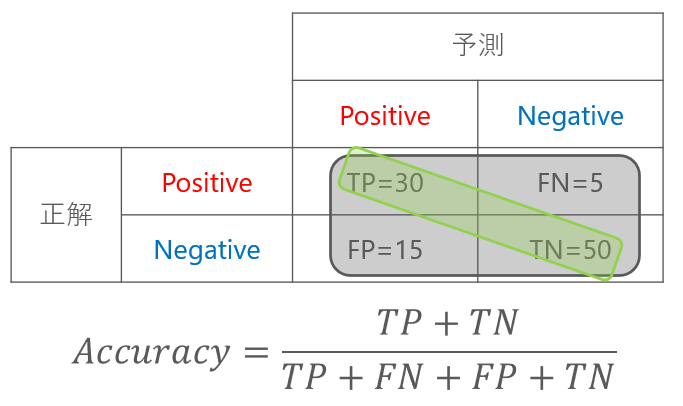
メールのスパム判定の例では、正解率は0.8となります。
正解率が適しているのは、PositiveとNegativeが同じくらいのときに使えます。
もし、PositiveかNegativeのどちらかに偏っていた場合、正解率は信用できなくなります。
たとえば、100個のデータのうち、Negativeが98個あったとします。
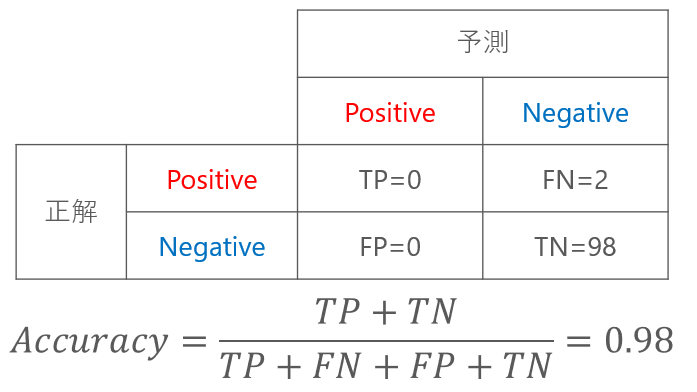
上の混同行列で、正解率は98%となっているので、一見すると性能が高いモデルのように思えます。
しかし、Positiveをまったく予測できていません。
適合率(Precision)
適合率とは、Positiveと判断したもののうち、本当にPositiveであったものの割合です。
メールがスパムであればPositiveなので、言い換えると、スパムと予測したもののうち、本当にスパムメールであった割合を示します。
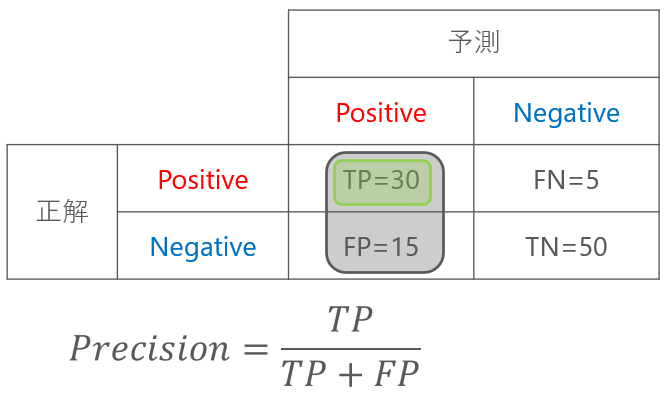
メールのスパム判定の例では、適合率は0.67となります。
適合率は、False Positiveをできるだけ減らしたい場合に有効です。
つまり、問題ないものを「問題あり」と判定するリスクを減らしたいときに、適合率を使います。
たとえば、スパムメールをフィルタリングするとき、通常メール(Negative)をスパムと判定することは避けたいです。
この場合は適合率が使われます。
再現率(Recall)
再現率とはPositiveをどれだけ再現できたか、つまり、機械学習モデルがPositiveのものを正しくPositiveと判定できた割合を表します。
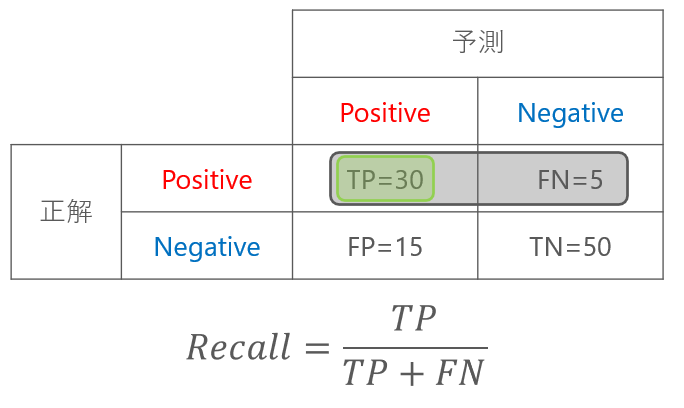
メールのスパム判定の例では、再現率は0.86となります。
再現率は、False Negativeをできるだけ減らしたい場合に有効です。
つまり、問題あるものを「問題なし」と判定するリスクを減らしたいときに、再現率を使います。
たとえば、病気のスクリーニング検査では、病気を見逃すと重大な結果を招きます。
この場合、本当は病気(Positive)なのに、病気でないと判定するリスクを減らしたいので、再現率を重視します。
F1スコア
今まで見たように、適合率(Precision)と再現率(Recall)には一長一短があります。
F1スコアは、適合率と再現率の平均をとった指標になります。
バランスをとっただけなので、解釈が難しいという欠点を抱えています。
計算方法は、適合率と再現率の調和平均をとります。
調和平均の理由ですが、適合率と再現率はどちらも比率を表しているからです。
比率の平均をとるときには調和平均が適しています。
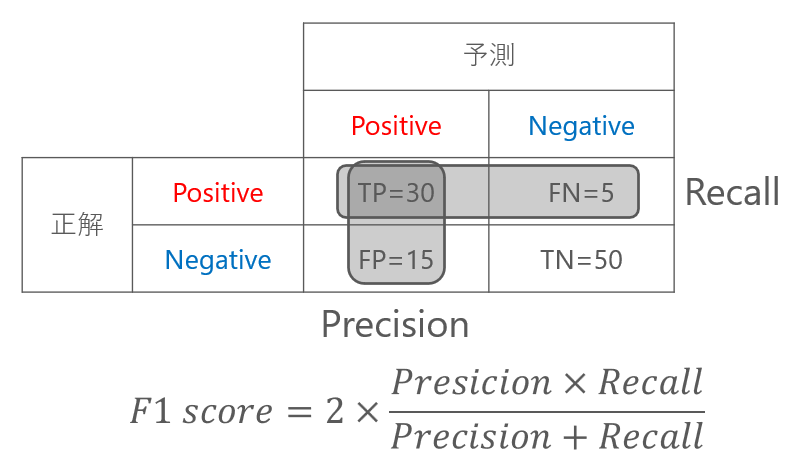
メールのスパム判定の例では、F1スコアは0.75となります。
F1スコアが使われる例としては、Positive/Negativeが偏っていて、FNとFPのどちらの誤分類も避けたいときがあります。
たとえば、詐欺検出システムで、不正取引(Positive)を正しく不正と判定し、かつ、通常取引(Negative)をまちがって不正と判定したくないときにF1スコアが使えます。
混同行列を使った評価指標として、ROC曲線が有名です。
ROC曲線は次の記事で解説しています。
まとめ
本記事では、混同行列の見方について解説しました。
最後に今までの説明をまとめます。
Positiveは問題あり、Negativeは問題なしを表します。
TP・TN・FP・FNの覚え方は、以下の通りとなります。
- 1文字目は、予測が正しいか(True)、まちがっているか(False)
- 2文字目は、本当はPositiveか、Negativeか
また、混同行列の性能をあらわす指標として、次のものがあります。
- 正解率は、全体の中で、正しく予測できた割合
- 適合率は、Positiveと予測したもののうち、本当にPositiveと予測できた割合
- 再現率は、本当はPositiveであるもののうち、Positiveと正しく予測できた割合
- F1スコアは、適合率と再現率の調和平均
混同行列は二値分類を評価するためによく使われるものなので、しっかり理解していきましょう。