母分散未知のときの区間推定の解き方

「母分散が未知のときの区間推定は、どうやって解けばいいの？」

こういった悩みを抱えていませんか？

実は、母分散未知の区間推定には公式が存在し、すぐに計算することができます。

この記事では、区間推定のやり方を具体例を使って解説します。

母分散未知の区間推定とは？

区間推定の公式の使い方を学ぶ前に、そもそも何を求めようとしているのでしょうか？

単に公式を覚えるだけでは、少し問題が変わっただけで応用できなくなってしまいます。

そのため、「母分散未知」と「区間推定」について理解していきましょう。

母分散未知とは

母分散とは、対象としている集団全体のばらつきの程度を表します。

下図のように、集団全体が中心付近に固まっていれば母分散は小さくなり、中心から離れれば母分散は大きくなります。

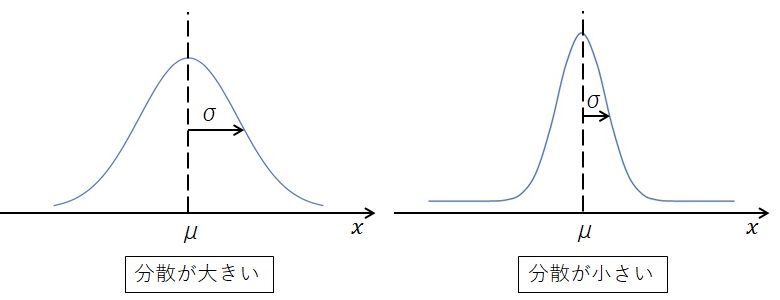
そして、母分散未知とは、上図で示したばらつきの程度が不明であるということです。

母分散が分からない状況でも推定を行えるのが、区間推定の魅力です。

区間推定とは(母分散未知の場合)

集団のばらつきの程度(母分散)が分かっていないのに、どうやって区間推定を行えるのでしょうか？

この問題を解決するために、集団から抽出したデータのばらつき(不偏分散)を計算して、不偏分散で母分散を代用します。

母分散の代わりに不偏分散を使うと、t 分布に従うという数学の定理があり、t 分布を使って区間推定を行います。

母分散未知の場合の信頼区間の求め方

信頼区間を求める公式を使うと簡単に計算することができます。

ただし、母分散既知と未知とでは公式が異なるので注意してください。

母分散既知の場合の公式は以下の記事で説明しています。

では、母分散未知の場合には、どのようにして信頼区間を求めるかを見ていきましょう。

信頼区間を求める公式

n 個のデータの平均値を \(\bar{X}\)、不偏分散を \(s^2\)とすると、母平均 \(\mu\) の信頼区間は下記の式で求めることができます。
$$\bar{X}-t \frac{s}{\sqrt{n}}\leq \mu \leq \bar{X}+t \frac{s}{\sqrt{n}}$$
ただし、s は母標準偏差(母分散の平行根)、t は信頼係数によって変化する値です。
t の値は、 t 分布表の自由度 n-1 を見て代入することになります。

例題で理解する公式の使い方

母分散が分かりませんので、前節の公式を使います。
$$\bar{X}-t \frac{s}{\sqrt{n}}\leq \mu \leq \bar{X}+t \frac{s}{\sqrt{n}}$$
この式を解くために必要なのは、データの平均、不偏分散、t の値の 3 つです。

それぞれを計算してみます。
\begin{align}
\bar{X}&=51.5\\
s^2&=7.17\\
t&=3.25
\end{align}
不偏分散の求め方は以下の記事で解説しています。

これらを公式に代入すると、
$$51.5-3.25 \frac{\sqrt{7.17}}{\sqrt{10}}\leq \mu \leq 51.5+3.25 \frac{\sqrt{7.17}}{\sqrt{10}}$$
式を整理して、
$$48.7 \leq \mu \leq 54.3$$

まとめ

本記事では、母分散が未知の場合の信頼区間の求め方を解説しました。

母分散が既知のときと未知のときとで、使う式が変わります。

母分散が未知のときの方が計算が大変ですが、公式に当てはめるだけですので、手を動かして公式の使い方をマスターしましょう。