はじめに
統計を勉強し始めると最初に登場する期待値。高校でも習うので「聞いたことある」と思う方も多いのではないでしょうか。
しかし、教科書では「期待値を~のように定義する」のように書かれていて、なぜそのように定義するのかについては書かれていないことがほとんどです。
定義なので覚える必要はありますが、丸暗記では時間が経つと忘れてしまいますし、意味も分からず覚えているとモヤモヤした感覚が残ると思います。
そこで、本記事では期待値がなぜそのように定義されているのかについて考えてみたいと思います。
また、期待値と平均の違いについても説明していきます。
期待値の定義
まず初めに、期待値の定義を確認しておきましょう。
確率変数を\(X\)、確率関数を\(f(x)\)、期待値を\(E(X)\)と表します。離散型と連続型の定義が存在します。
\(X\)が離散型確率変数の場合
$$E(X)=\sum_{x_i} x_i f(x_i)$$
\(X\)が連続型確率変数の場合
$$E(X)=\int_{-\infty}^{\infty} x f(x) dx$$
どちらの定義も表していることは同じで、確率変数が取り得る値に、その確率をかけて総和を取ったものになっています。
…といっても、この説明では意味が分かりませんので、具体例を使って期待値の定義とは何を表しているのかについて考えていきたいと思います。
具体例から考える期待値の定義の意味
期待値の定義を考えるために、次のような例を考えてみます。
さいころを1回投げて、1~3の目が出ると1点、4~5の目が出ると2点、6の目が出ると3点もらえる。得点\(X\)の期待値は?
例題を表にすると、下図のようになります。
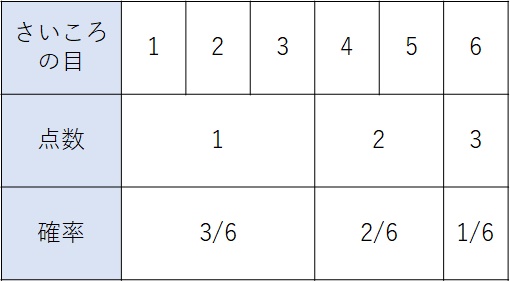
このグラフから、確率変数\(X\)を代表する値(期待値)を考えてみたいと思います。
期待値の定義に従って計算すると、
\begin{align}
E(X)&=\left( 1\times \frac{3}{6} \right) + \left( 2\times \frac{2}{6} \right) + \left( 3\times \frac{1}{6} \right)\\
&\cong 1.7
\end{align}
となります。ここでは計算結果よりも、途中式に着目してみましょう。
期待値とは、確率分布(上図)を表す代表的な値ですから、確率が大きな値ほど重要であることは容易に想像できます。
そこで、確率を重みづけとして見てみましょう。つまり、括弧の中を
\[取り得る値 \times その値の重要度\]
と見てみます。すると、期待値の途中計算は、
「値1の重要度は\( \frac{3}{36} \)、値2の重要度は\( \frac{2}{36} \)、値3の重要度は\( \frac{1}{36} \)」
というように捉えられます。
確率を重要度として見なすと、期待値の計算式の意味がおぼろげながらも分かってくると思います。
期待値と平均の違い
さて、最後に期待値と平均の違いについて説明します。
期待値のことを平均と呼ぶことがあるので、両者の厳密な意味は同じかもしれませんが、私たちが普段使う平均とは、
全部のデータを足して、データの個数で割った値
のことを表します。このことを次の例で確認してみましょう。
さいころを1回投げて、1~2の目が出ると1点、3~4の目が出ると2点、5~6の目が出ると3点もらえる。得点\(Y\)の平均は?
先ほどの例題の点数を変えただけです。この得点と確率は下の表のようになります。
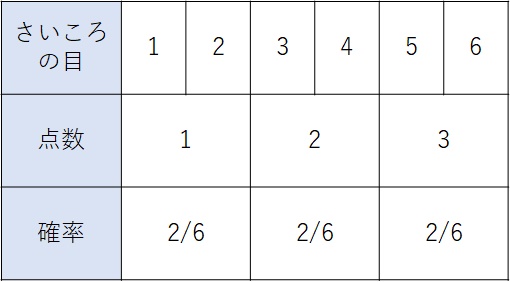
では、平均と期待値の違いを説明するために、まずは平均を計算してみます。
平均は、点数の和をデータの数で割ればよいので、
\begin{align}
平均&=\frac{1+2+3}{3}\\
&=2\\
\end{align}
です。分母の3は、「点数が1、2、3の3通りある」という意味です。平均の式を次のように変形してみましょう。
\begin{align}
平均&=\left( 1\times \frac{1}{3} \right) + \left( 2\times \frac{1}{3} \right) + \left( 3\times \frac{1}{3} \right)\\
&=\left( 1\times \frac{2}{6} \right) + \left( 2\times \frac{2}{6} \right) + \left( 3\times \frac{2}{6} \right)\\
\end{align}
こうすると、最後の式は期待値の定義そのものになっています。
つまり平均とは、「期待値を計算するときの重要度がすべて同じ」ことを意味しています。
例題では、「点数1、2、3を取る確率はすべて等しい」から、平均と期待値の計算結果が同じになります。
逆に言うと、例1のような「点数1、2、3を取る確率が異なる」場合には、平均と期待値は一致しません。
ただし、人によっては期待値のことを平均と呼ぶ場合もあるので、平均を次のどちらで定義するのかは自分の中で決めておいた方がいいと思います。
(1)(期待値の定義と同じ)
\(\displaystyle 平均=\sum_{x_i} x_i f(x_i)\)
(2)(小学校で習う定義)
平均=(データをすべて足したもの)÷(データ数)
(1)の定義の場合、期待値と平均の意味は全く同じです。(2)の場合、例2で述べたように、各データがとる確率がすべて等しい場合のみ、期待値と平均が同じになります。
平均の定義(1)、(2)のどちらが良いということはなく、個人の好みの問題ですので、覚えやすいほうの定義を選ぶと良いと思います。
おわりに
いかがだったでしょうか。今回は期待値の定義と、平均との違いについて説明しました。
筆者自身、「期待値の計算はできるけど、単に定義を暗記しているだけ」の状態で、ずっと心の中にモヤモヤした感情を抱えていました。
この記事が皆さんの理解の一助になれば幸いです。

