ヒストグラムから中央値を求めるのが難しくて悩んでいませんか?
本記事では、中央値の求め方を丁寧に解説していきます。
ヒストグラムから中央値を計算する手順
次の例題を使って考えてみます。
ある学校の生徒 30 人が国語のテストを受けた。
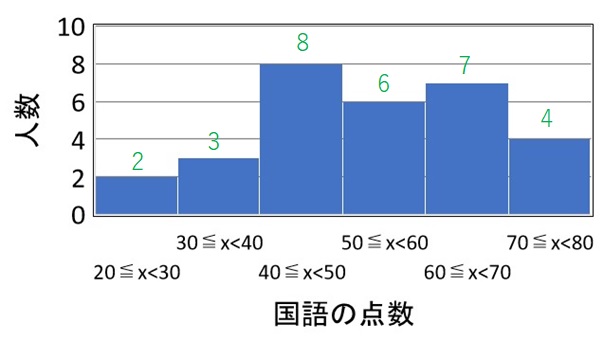
国語の点数の分布は以下のグラフのようになっていた。
30 人のテストの中央値は?
まず初めに、中央値とは
「データを小さい順に並べたとき、中央にあるデータ」
のことを指します。
中央値を求めるときには、グラフで考えるよりも、表で考える方が分かりやすいです。
そのため、例題のヒストグラムを表にしたものを下記に示します。
| 点数(階級) | 人数(度数) |
|---|---|
| 20 ≦ x < 30 | 2 |
| 30 ≦ x < 40 | 3 |
| 40 ≦ x < 50 | 8 |
| 50 ≦ x < 60 | 6 |
| 60 ≦ x < 70 | 7 |
| 70 ≦ x < 80 | 4 |
手順1 累積度数を計算する
累積度数とは、各区間の度数を足したものになります。
| 点数(階級) | 人数(度数) | 累積度数 |
|---|---|---|
| 20 ≦ x < 30 | 2 | 2 |
| 30 ≦ x < 40 | 3 | 5 |
| 40 ≦ x < 50 | 8 | 13 |
| 50 ≦ x < 60 | 6 | 19 |
| 60 ≦ x < 70 | 7 | 26 |
| 70 ≦ x < 80 | 4 | 30 |
例えば、「20 ≦ x < 30」には 2 人、「30 ≦ x < 40」には 3 人いるので、40 点未満の生徒は合計 5 人いることが分かります。
このことを、表の中では「30 ≦ x < 40」の累積度数の欄に「5」と書いています。
手順2 区間の最大値と、累積度数を取った折れ線グラフを描く
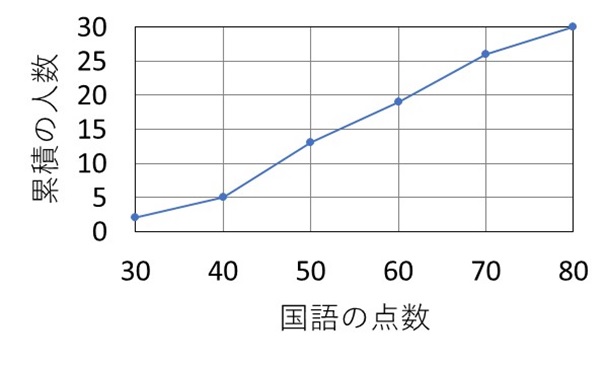
横軸に各区間の最大値、縦軸に累積度数を取ってグラフを描きます。
このグラフを見ると、40 点未満の生徒が 5 人ということがすぐに分かります。
手順3 累積度数の中央の値を読み取る
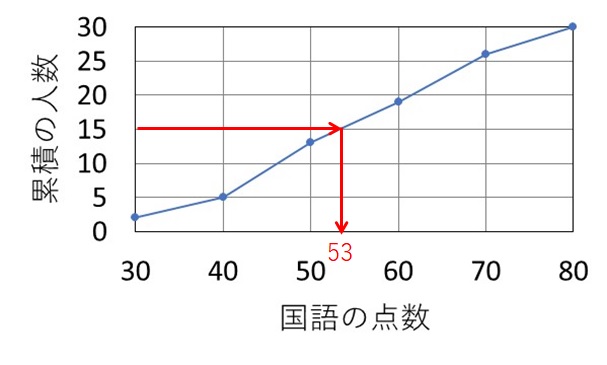
生徒の数は全員で 30 人ですので、中央の値である 15 番目の点数を読み取ります。
上図のように累積度数が 15 の値を読み取ると、53 点ということが分かります。
よって、国語の点数の中央値は 53 点です。
まとめ
本記事では、ヒストグラムから中央値を求める方法について解説しました。
中央値を求めるためには、3 つの手順に沿って計算する必要があり、手間がかかります。
本来、中央値を求めるためにはデータを小さい順に並び替えて、真ん中の値を読み取れば良いです。
しかし、ヒストグラムでは各々の生徒が何点を取ったのか、というデータがないので、回り道をして解かなければなりません。
計算方法が分からなくなったときに、本記事を参考にしてください。


