「平均」という言葉には馴染みがあると思いますが、平均には 3 種類あることはご存知でしょうか?
その 3 種類とは算術平均、幾何平均、調和平均です。
本記事では、算術平均と幾何平均の違いについて詳しく解説します。
幾何平均と算術平均の意味
算術平均とは
算術平均とは、「値そのものの平均」のことを指します。
5 つのデータ \(x_1, x_2, \cdots, x_5\) があるとき、算術平均 \(\bar{x}\) は次のように計算できます。
$$\bar{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$$
算術平均は、皆さんが日常生活で思い浮かべる「平均」と合致するのではないでしょうか。
ここで、後の幾何平均との違いを明確にするため、算術平均の計算式を変形します。
\begin{align}
5\bar{x}&=x_1+x_2+x_3+x_4+x_5\\
\bar{x}+\bar{x}+\bar{x}+\bar{x}+\bar{x}&=x_1+x_2+x_3+x_4+x_5
\end{align}
つまり、算術平均の和と、全部のデータの和が一致します。
幾何平均とは
幾何平均とは、「変化率の平均」のことを指します。
変化率が \(r_1, r_2, \cdots, r_5\) と書けるとき、幾何平均 \(r\) は次のように計算できます。
$$r=\sqrt[5]{r_1r_2r_3r_4r_5}$$
ここで、\(\sqrt[5]{t}\) の記号は「5 乗根」と呼ばれ、
$$(\sqrt[5]{t})^5=t$$
という関係が成り立ちます。
さて、前節と同じように、幾何平均の式を変形してみます。
両辺を 5 乗すると、以下のように表されます。
$$r^5=r_1r_2r_3r_4r_5$$
この式を見ていただくと分かるように、幾何平均の積と、全部のデータの積が一致します。
つまり、算術平均と幾何平均の計算式の違いは、
- (算術平均の和)=(データの和)
- (幾何平均の積)=(データの積)
です。このように対応させると忘れにくくなります。
では、算術平均と幾何平均は実際にどのように使い分けられるのか、例を見てみましょう。
幾何平均と算術平均の使い分けの例
2 つの平均をどのように使い分けるのかを理解するため、次の例題を考えてみます。
A社が作っている商品の売上は下図に示すようになっている。
5 年間の商品の売上の平均、および売上の変化率の平均を求める。
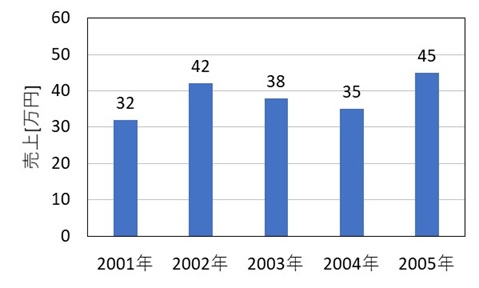
「5 年間の商品の売上の平均」は算術平均で求めることができます。
「5 年間の商品の売上の変化率の平均」は幾何平均で求めることができます。
算術平均の求め方
算術平均は、5 年間の売上をならしたイメージです。
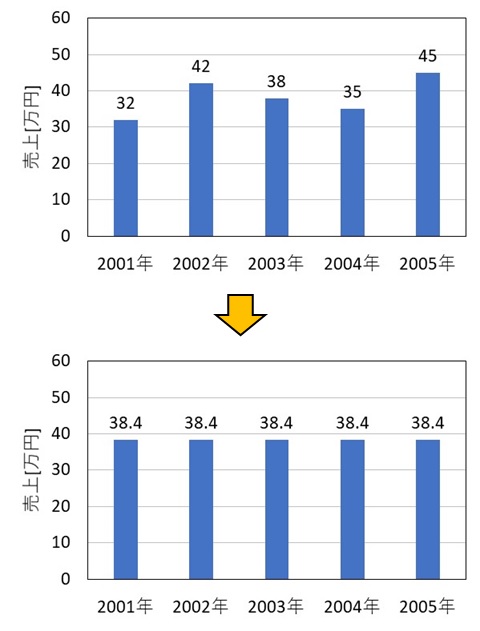
計算式に当てはめてみると、
\begin{align}
\bar{x}&=\frac{32+42+38+35+45}{5}\\
&=38.4
\end{align}
となります。つまり、5 年間の売上の平均は 38.4 万円です。
幾何平均の求め方
幾何平均は、一定の割合で増えていく、というイメージで捉えると理解しやすいです。
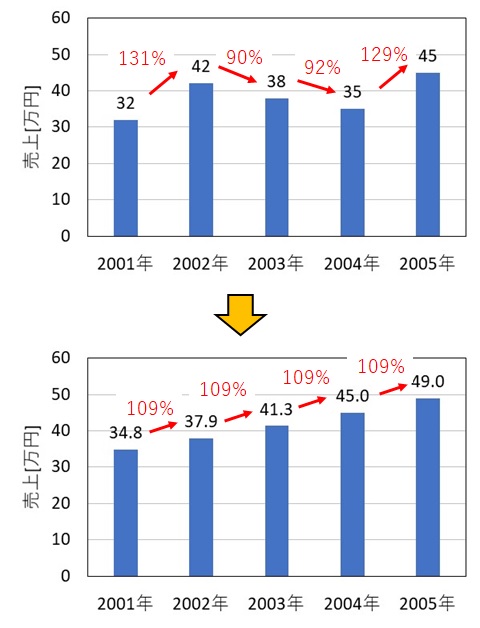
各年の売上の変化率は上図のように、\( (131\%,90\%,92\%,129\%) \) となります。
売上のデータは全部で 5 つありますが、変化率は 4 つになります。
幾何平均を計算すると、
\begin{align}
r&=\sqrt[4]{131\times90\times92\times129}\\
&=109
\end{align}
つまり、 5 年間の平均変化率は 109%ということが分かります。
まとめ
本記事では、算術平均と幾何平均の違いを解説しました。
それぞれの意味は、
- 算術平均:値そのものの平均
(算術平均の和)=(データの和) - 幾何平均:値の変化率の平均
(幾何平均の積)=(データの積)
です。
使う場面が異なりますので、正しく使い分けられるようになりましょう。


